决策树算法-c4.5

## 1 问题背景

**id3 算法**具有如下缺点：

1. 没有剪枝策略，容易过拟合。
2. 信息增益准则对可取数目较多的特征有所偏好，类似“编号”的特征其信息增益接近于 1。
3. 只能用于处理离散分布的特征。
4. 没有考虑缺失值。

针对**id3 算法**的不足，Quinlan 又提出了**C4.5 算法**，C4.5 算法采用**信息增益率**来取代**信息增益**作为当前最优决策属性的度量标准。

仍然选择**weka**中天气的数据集为例子：

| outlook  | temperature | humidity | windy | play |
| -------- | ----------- | -------- | ----- | ---- |
| sunny    | hot         | high     | FALSE | no   |
| sunny    | hot         | high     | TRUE  | no   |
| overcast | hot         | high     | FALSE | yes  |
| rainy    | mild        | high     | FALSE | yes  |
| rainy    | cool        | normal   | FALSE | yes  |
| rainy    | cool        | normal   | TRUE  | no   |
| overcast | cool        | normal   | TRUE  | yes  |
| sunny    | mild        | high     | FALSE | no   |
| sunny    | cool        | normal   | FALSE | yes  |
| rainy    | mild        | normal   | FALSE | yes  |
| sunny    | mild        | normal   | TRUE  | yes  |
| overcast | mild        | high     | TRUE  | yes  |
| overcast | hot         | normal   | FALSE | yes  |
| rainy    | mild        | high     | TRUE  | no   |

## 2 预测过程

### 2.1 计算属性 outlook 的信息增益

$$
Gain(S, outlook)=Entropy(S)-Entropy(outlook)=0.24675
$$

### 2.2 计算属性 outlook 的分裂信息量

$$
{Split(outlook)}=-\sum_{i=1}^k\frac{\vert S_i\vert}{\vert S\vert}\log\frac{\vert S_i\vert}{\vert S\vert}
$$

通过 outlook 将样本分为以下几个部分：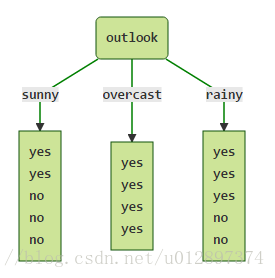

![20170711161436317 (275×278)](/media/202103/2021-03-31_151028.png)

因此 $Split(outlook)$ 为：

$$
Split(outlook)=-\frac5{14}\times\log_2\frac5{14}-\frac4{14}\times\log_2\frac4{14}-\frac5{14}\times\log_2\frac5{14}=1.577
$$

### 2.3 计算属性 outlook 的信息增益率

$$
Gain_\_ratio(outlook)=\frac{Grain(S,outlook)}{Split(outlook)}=\frac{0.24675}{1.577}=0.155
$$

同理，其他属性的信息增益率为：

$$
\begin{array}{l}Grain_\_ratio(temperature)=\frac{0.029}{1.556}=0.0186\\Grain_\_ratio(humidity)=\frac{0.151}{1.0}=0.151\\Grain_\_ratio(windy)=\frac{0.048}{0.985}=0.048\end{array}
$$

### 2.4 总结

由此可见，属性 outlook 的信息增益率最大，因此第一步选择该属性为分类属性。在分裂之后的子节点中，如果该子节点只有一种 $label$，则停止继续分类。否则重复上述步骤，继续分裂下去。

## 3 处理连续型属性

C4.5 算法中的策略是采用二分法将连续属性离散化处理，具体过程如下：

1. 假定样本集 $D$ 的连续属性 $a$ 有 $n$ 个不同的取值，对这些值**从小到大**排序，得到属性值的集合 $\{a_1,a_2,...,a_n\}$。
2. 把区间 $[a_i,a_{i+1})$ 的中位点 $\frac{a_i+a_{i+1}}{2}$ 作为候选划分点，于是得到包含 $n-1$ 个元素的划分点集合：

$$
T_a=\{\frac{a_1+a_{i+1}}2\vert1\leq i\leq n-1\}
$$

3. 基于每个划分点 $t$，可将样本集 $D$ 分为子集 $D_t^-$ 和 $D_t^+$，其中 $D_t^-$ 中包含属性 $a$ 上不大于 $t$ 的样本，$D_t^+$ 包含属性 $a$ 大于 $t$ 的样本。
4. **对于每个划分点 $t$，计算其信息增益，然后选择使信息增益最大的划分点进行样本集合的划分**。
5. 然后计算**最佳划分点**的**信息增益率**作为连续属性 $a$ 的信息增益率。

## 4 处理缺失值

现实任务中，通常会遇到大量不完整的样本，如果直接放弃不完整的样本，对数据是极大的浪费，例如下面这个有缺失值的西瓜样本集，只有 4 个完整样本。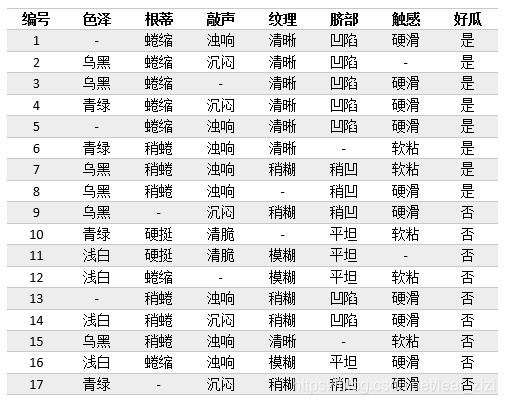

![20181030155333232.jpg (505×404)](/media/202103/2021-03-31_165845.png)

**对于有缺失值的属性，其信息增益就是无缺失值样本所占的比例乘以无缺失样本子集的信息增益**：

$$
Gain(D,a)=\mathcal l\times{Gain(\widetilde D,a)}
$$

其中：$\mathcal l$ 是属性 $a$ 上无缺失值样本所占的比例；$\widetilde D$ 是属性 $a$ 上无缺失值的样本子集。

下面首先计算属性 `色泽` 的信息增益：

![](/media/202103/2021-03-31_172835.png)

然后计算属性 `色泽` 的分裂信息量，此时将缺失值当做一种单独的属性：

$$
Split(a)=-\frac4{17}log_2\frac4{17}-\frac6{17}log_2\frac6{17}-\frac4{17}log_2\frac4{17}-\frac3{17}log_2\frac3{17}
$$

最后计算 `色泽` 的信息增益率：

$$
Grain\_ratio(a)=\frac{Gain(D,a)}{Split(a)}
$$

然后再根据信息增益率的大小选择最优划分属性，确定之后再按照上述步骤依次寻找其他划分属性即可。

## 5 剪枝

C4.5算法采用**悲观错误剪枝（Pessimistic Error Pruning，PEP）**方法进行剪枝，具体的剪枝原理及方法可以参考[2.1.5 剪枝处理的作用及策略](http://notebook.ricear.com/project-24/doc-245)中的`2.2.1.2 悲观错误剪枝-PEP`。

## 6 参考文献

1. [C4.5(weka 又称为 J48)算法原理详解](https://blog.csdn.net/u012897374/article/details/74983742?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-3.control&dist_request_id=1328761.94.16171635574583771&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-3.control)。
2. [分类算法之决策树 C4.5 算法](https://blog.csdn.net/qq_36330643/article/details/77444048?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161716255116780271595516%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=161716255116780271595516&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_v29-1-77444048.pc_v2_rank_blog_default&utm_term=c4.5&spm=1018.2226.3001.4450)。
3. [机器学习笔记（5）——C4.5 决策树中的连续值处理和 Python 实现](https://blog.csdn.net/leaf_zizi/article/details/83105836)。