Bagging和Boosting的联系与区别

## 1 Bagging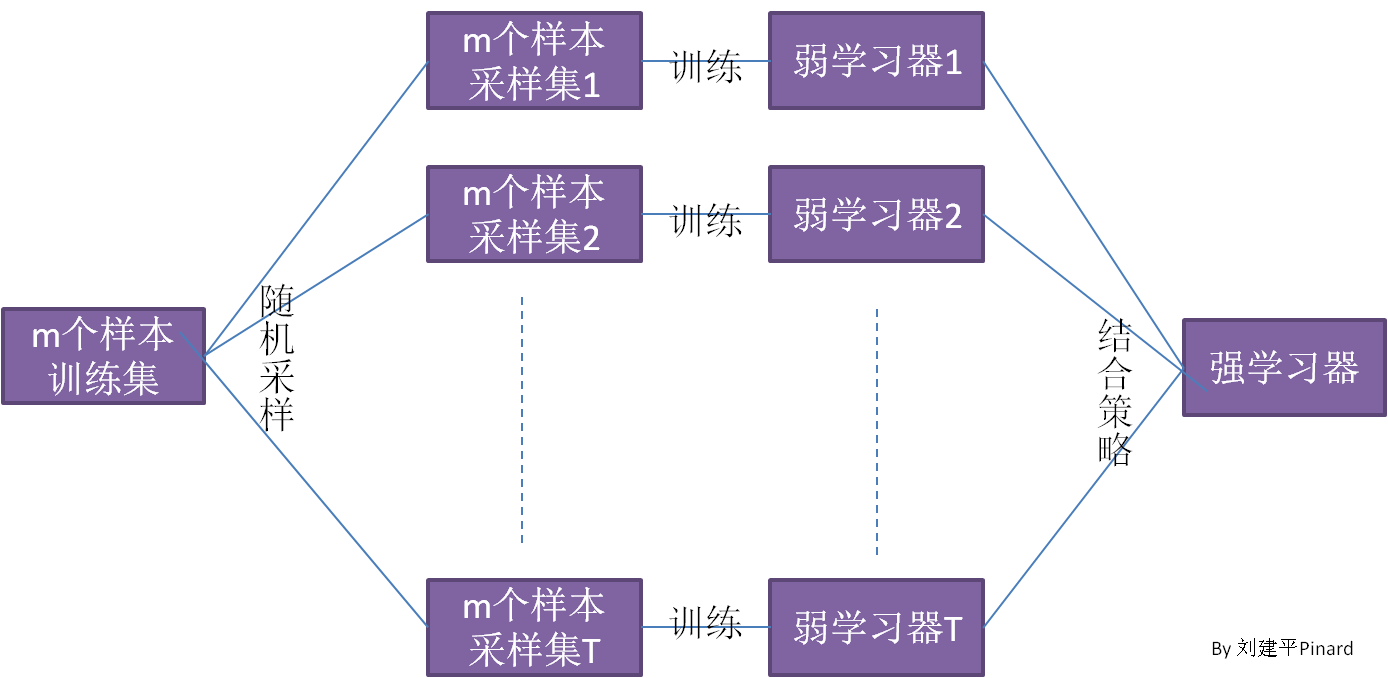

![1042406-20161204200000787-1988863729.png (1388×678)](/media/202104/2021-04-04_142757.png)

1. **Bagging**的个体弱学习器的训练集是通过随机采样得到的，这里一般采用的是**自助采样法**（Bootstrap Sampling），Bagging 对于弱学习器没有限制，但是常用的一般是**决策树**和**神经网络**。
2. 通过 $T$ 次的随机采样，我们就可以得到 $T$ 个采样集。
3. 对于这 $T$ 个采样集，我么可以分别独立的训练出 $T$ 个弱学习器，再对这 $T$ 个弱学习器通过集合策略来得到最终的学习器。**Bagging**的结合策略也比较简单，具体如下：
   1. 对于**分类问题**，通常使用**简单投票法**，得到最多票数的类别或者类别之一为最终的模型输出。
   2. 对于**回归问题**，通常使用**简单平均法**，对 $T$ 个弱学习器得到的回归结果进行算术平均得到最终的模型输出。
4. 由于 Bagging 算法**每次都进行采样来训练模型**，因此**泛化能力很强**，对于降低模型的方差很有作用，但是**对于训练集的拟合程度就会差一些**，也就是**模型的偏倚会大一些**。

Bagging 系列算法中主要的算法有**随机森林**算法。

> 自助采样法：
> 
> * 对于 $m$ 个样本的原始训练集，我们每次先随机采集一个样本放入采样集，接着**把该样本放回**，也就是说下次采样时该样本仍有可能被采集到。
> * 这样采集 $m$ 次，最终可以得到 $m$ 个样本的采样集，由于是随机采样，这样每次的采样集和原始训练集是不同的，和其他采样集也是不同的，这样就可以得到多个不同的弱学习器。
> * 对于一个样本，它在某一次含 $m$ 个样本的训练集的采样中，每次被采到的概率是 $\frac1m$，不被采到的概率为 $1-\frac1m$，则 $m$ 次采样都没有被采中的概率是 $(1-\frac1m)^m$。当 $m\rightarrow\infty$ 时，$(1-\frac1m)^m\rightarrow\frac1e\approx0.368$。也就是说，在 bagging 的每轮随机采样中，训练集中大约有 36.8% 的数据没有被采样集采集中。对于这部分大于 36.8% 的没有被采集到的数据，我们常常称之为袋外数据（Out of Bag，简称 OOB）。这些数据没有参与训练集模型的拟合，因此可以用来检测模型的泛化能力。

## 2 Boosting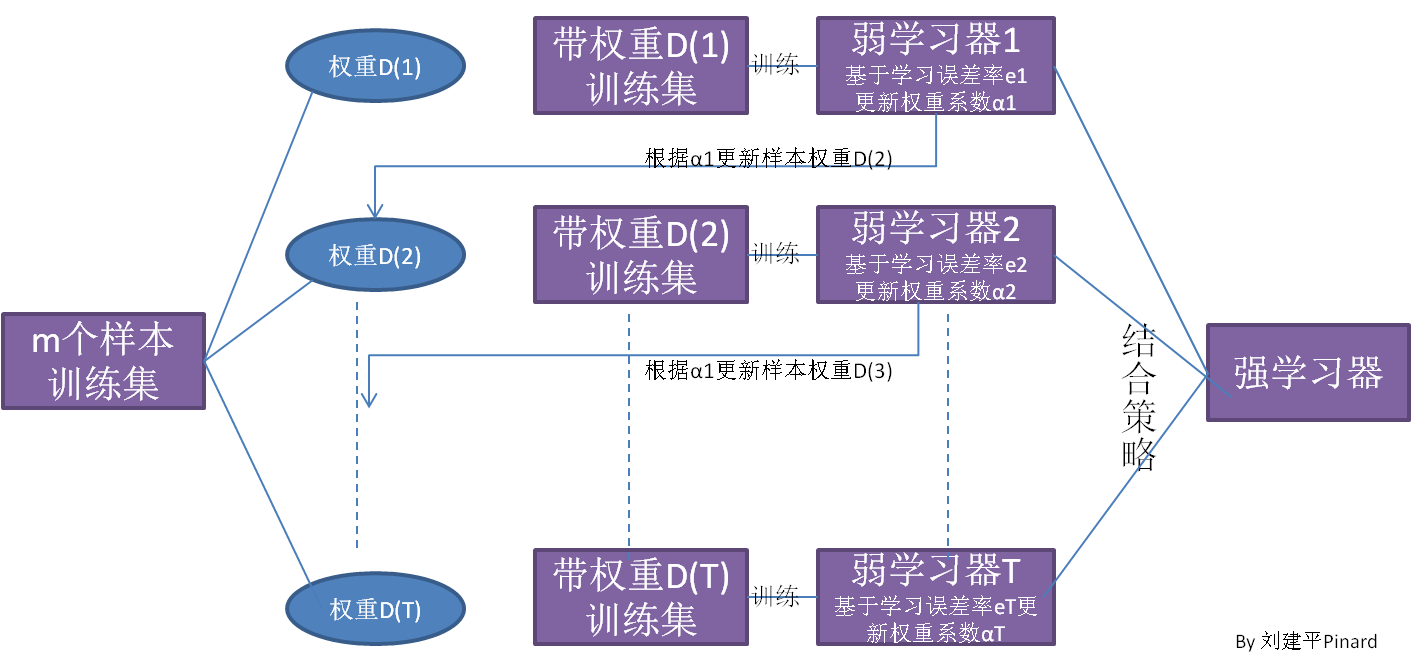

![](/media/202104/2021-04-04_155236.png)

Boosting 算法的原理如下：

1. 首先从训练集用初始权重训练出一个弱学习器 1，根据弱学习的学习误差率表现来更新训练样本的权重，**使得之前弱学习器 1 学习误差率高的训练样本点的权重变高。使得这些误差率高的点在后面的弱学习器 2 中得到更多的重视**。
2. 然后基于**调整权重后的训练集**来训练弱学习器 2。
3. 如此反复进行，直到**弱学习器数达到事先指定的数目 T**，最终将这 $T$ 个弱学习器通过集合策略进行整合，得到最终的强学习器。

Boosting 系列算法里最著名的算法有**AdaBoost**算法和**提升树**（Boosting Tree）算法。提升树系列算法里面应用最广泛的是**梯度提升树**（Gradient Boosting Tree）。

## 3 Bagging 和 Boosting 的区别

1. **样本选择上：**
   1. Bagging：训练集是在原始训练集中有放回选取的，从训练集中选出的各轮训练集之间是独立的。
   2. Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化，而权值是根据上一轮的分类结果进行调整。
2. **样例权重：**
   1. Bagging：使用均匀抽样，每个样例的权重相等。
   2. Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。
3. **预测函数：**
   1. Bagging：所有预测函数的权重相等。
   2. Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。
4. **并行计算：**
   1. Bagging：各个预测函数可以并行生成。
   2. Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

## 4 参考文献

1. [集成学习原理小结](https://www.cnblogs.com/pinard/p/6131423.html)。
2. [Bagging 与随机森林算法原理小结](https://www.cnblogs.com/pinard/p/6156009.html)。
3. [Bagging 和 Boosting 的区别（面试准备）](https://www.cnblogs.com/earendil/p/8872001.html)。