决策树算法-cart

## 1 概述

* **Classification And Regression Tree**，即**分类回归树**算法，简称**CART 算法**。
* 它是决策树的一种实现，通常决策树有三种实现，分别是**ID3 算法、C4.5 算法、CART 算法**。
* **CART 算法**是一种**二分递归分割**技术，把当前样本划分为**两个子样本**，使得生成的**每个非叶子节点都有两个分支**，因此，CART 算法生成的决策树是结构简介的**二叉树**。
* 由于 CART 算法构成的是一个二叉树，他在每一步决策时只能`是` 或者`否`，**即使一个属性有多个取值，也是把数据分为两个部分**。
* 在 CART 算法中，主要分为两个步骤：
  1. 决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大。
  2. 决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这是损失函数最小作为剪枝标准。

## 2 优缺点

### 2.1 优点

1. 计算简单，易于理解，可解释性强。
2. 比较适合处理**有缺失属性的样本**。
3. 不仅能够处理不相关的特征，还能在相对短的时间内对大型数据源得出可行且效果良好的结果。

### 2.2 缺点

1. 不支持在线学习，在有新的样本产生后，决策树模型要重建。
2. 容易出现过拟合的现象，生成的决策树可能对训练数据有良好的分类能力，但对未知的测试数据却未必有很好的的分类能力。

## 3 与 C4.5 算法的区别

1. **C4.5 算法**采用**信息增益率**来作为分支特征的选择标准，而**CART 算法**则采用**Gini 系数**。
2. **C4.5 不一定是二叉树，但 CART 一定是二叉树。**

## 4 算法原理

1. 设节点的训练数据集为 $D$，计算现有特征对该数据集的 $Gini$ 系数。此时，对每一个特征 $A$，对其可能取的每个值 $a$，根据样本点对 $A=a$ 的测试为 `是` 或`否` 将 $D$ 分割成 $D_1$ 和 $D_2$ 两个部分，计算 $A=a$ 时的 $Gini$ 系数。
2. 在所有可能的特征 $A$ 以及他们所有可能的切分点 $a$ 中，选择 $Gini$ 系数最小的特征及其对应的切分点作为最有特征与最优切分点。
3. 依据最优特征与最优切分点，从现节点生成两个子节点，将训练数据集依特征分配到两个子节点中去。
4. 对两个子节点递归地调用步骤 1~3，直至满足停止条件。
5. 生成 CART 决策树

算法停止计算的条件有如下几个：

1. 样本个数小于预定阈值。
2. 样本集的 $Gini$ 系数小于预定阈值（样本基本属于同一类）。
3. 没有更多特征。

## 5 实例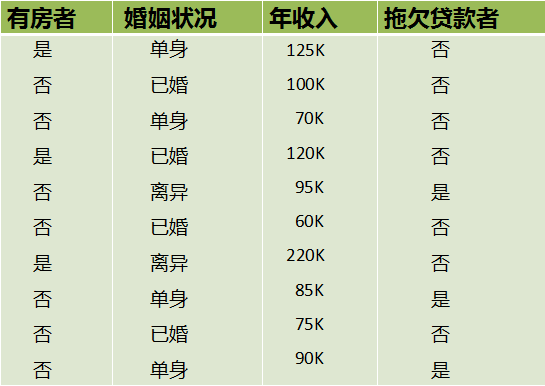

![v2-d2b03f1fc575b896c32aac12de8a3558_1440w.jpg (545×386)](/media/202104/2021-04-02_171312.png)

数据如上图所示，该数据具有如下特征：

1. 属性有三个，分别是**有房情况**、**婚姻状况**和**年收入**。
2. 有房情况和婚姻状况是离散的取值，而年收入是连续的取值。
3. 拖欠贷款者属于分类的结果。

下面开始进行具体的计算：

### 5.1 建树

1. 假设现在来看有房情况这个属性，那么按照他划分后的 $Gini$ 指数计算如下：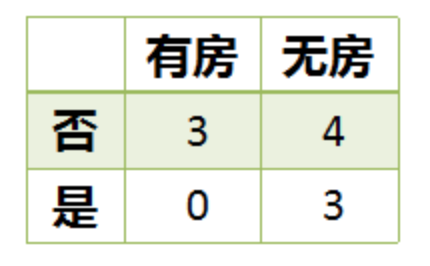

![](/media/202104/2021-04-02_171837.png)

$$
Gini(t_1)=1-(\frac33)^2-(\frac03)^2=0
$$

$$
Gini(t_2)=1-(\frac47)^2-(\frac37)^2=0.4849
$$

$$
Gini(有房情况)=0.3\times0+0.7\times0.44898=0.343
$$

2. 而对于婚姻状况来说，他的取值有 3 种，按照每种属性值分裂后 $Gini$ 指标计算如下：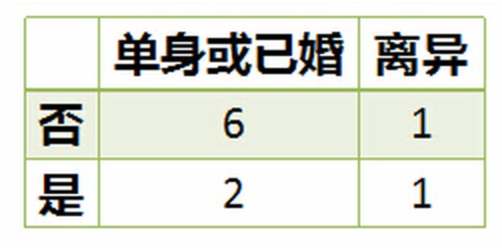

![](/media/202104/2021-04-02_172320.png)

$$
Gini(t_1)=1-(\frac68)^2-(\frac28)^2=0.375
$$

$$
Gini(t_2)=1-(\frac12)^2-(\frac12)^2=0.5
$$

$$
Gini(婚姻状况 1)=\frac8{10}\times0.375+\frac2{10}\times0.5=0.4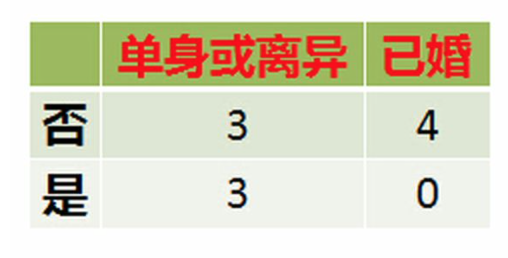
$$

![](/media/202104/2021-04-02_172756.png)

$$
Gini(t_1)=1-(\frac36)^2-(\frac36)^2=0.5
$$

$$
Gini(t_2)=1-(\frac44)^2-(\frac04)^2=0
$$

$$
Gini(婚姻状况 2)=\frac6{10}\times0.5+\frac4{10}\times0=0.3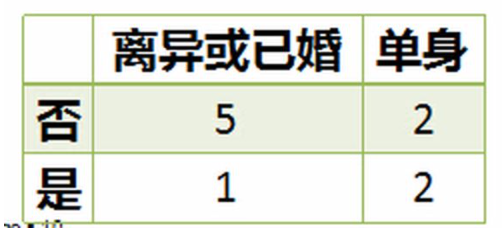
$$

![](/media/202104/2021-04-02_173224.png)

$$
Gini(t_1)=1-(\frac56)^2-(\frac16)^2=0.2778
$$

$$
Gini(t_2)=1-(\frac24)^2-(\frac24)^2=0.5
$$

$$
Gini(婚姻状况3)=\frac6{10}\times0.2778+\frac4{10}\times0.5=0.3667
$$

3. 最后还有一个取值连续的属性，年收入，他的取值是连续的，那么连续的取值采用**分裂点**来进行分裂，具体如下：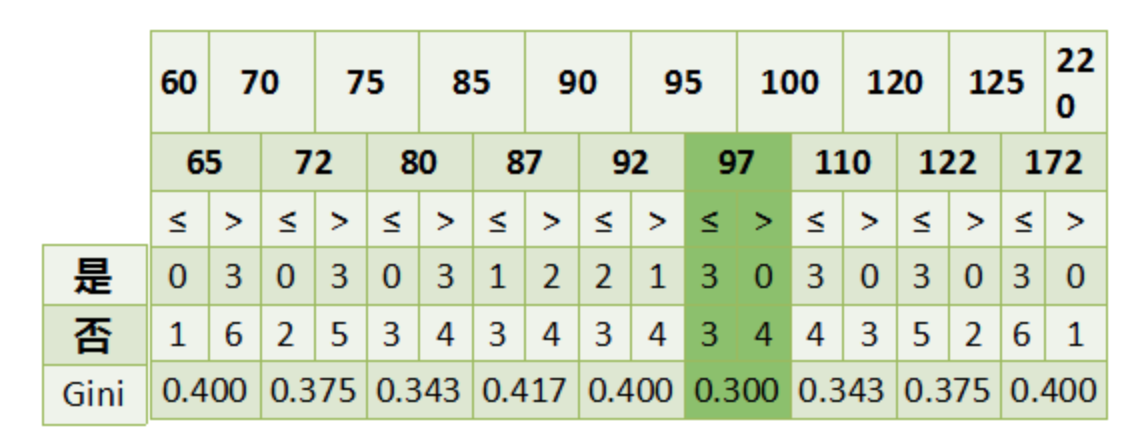

![](/media/202104/2021-04-02_173628.png)

4. 根据这样的分裂规则CART算法就能完成建树过程了。

### 5.2 剪枝

建树完成后就要进行第二步**剪枝**了，即根据验证数据进行剪枝。CART算法采用**代价复杂度剪枝法，即CCP**，具体可参见[2.1.5 剪枝处理的作用及策略](http://notebook.ricear.com/project-24/doc-245)中的 `2.2.1.3 代价复杂度剪枝-CCP`。

## 6 参考文献

1. [CART算法](https://zhuanlan.zhihu.com/p/32003259)。
2. [CART树算法详解](https://blog.csdn.net/e15273/article/details/79648502)。
3. [数据挖掘十大算法—— CART](https://zhuanlan.zhihu.com/p/74727025)。