Machine Learning
1、基础知识
1.1 机器学习方式
1.2 模型评估
1.2.1 错误率与精度
1.2.2 查准率与查全率
2、分类-基本算法
2.1 决策树
2.1.1 决策树的基本原理
2.1.2 决策树的三要素
2.1.3 决策树算法的优缺点
2.1.4 熵和信息增益的区别
2.1.5 剪枝处理的作用及策略
2.1.6 决策树算法-id3
2.1.7 决策树算法-c4.5
2.1.8 决策树算法-cart
3、分类-组合算法
3.1 集成学习概述
3.2 个体学习器
3.3 结合策略
3.4 Bagging和Boosting的联系与区别
3.5 Bagging
3.5.1 随机森林原理
3.6 Boosting
3.6.1 AdaBoost原理
-
+
游客
注册
登录
随机森林原理
## 1 含义 **随机森林**就是通过集成学习的思想将多棵树集成的一种算法,本质上是将**完全生长的 CART 决策树**通过**Bagging**的形式结合起来,得到一个庞大的决策模型。 > **Bagging**和**Decision Tree**算法各自具有一个很重要的特点: > > 1. **Bagging 具有减少不同 $g_t$ 的方差的特点。** 这是因为 Bagging 采用投票的形式,将所有 $g_t$ 结合起来,起到了求平均的作用,从而降低方差。 > 2. **Decision Tree 具有增大不同 $g_t$ 的方差的特点。** 这是因为 Decision Tree 每次切割的方式不同,而且分支包含的样本数在逐渐减少,所以他对不同的资料 $D$ 会比较敏感一些,从而不同的 $D$ 会得到比较大的方差。 ## 2 构造过程 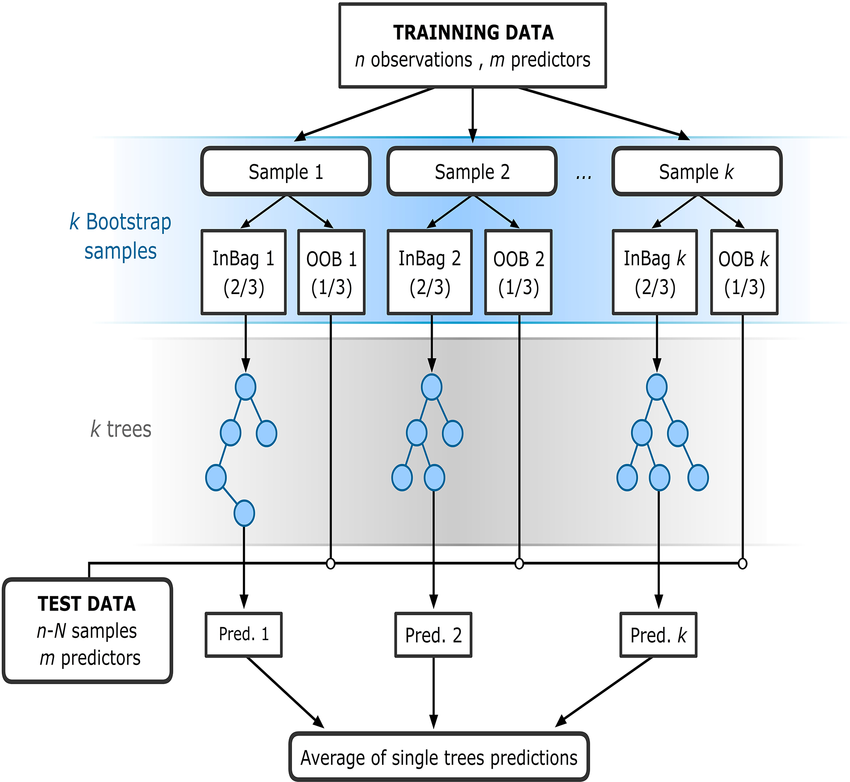 随机森林的构造过程如下: 1. 一个样本容量为 $N$ 的样本,有放回的抽取 $N$ 次,每次抽取 1 个,最终形成了 $N$ 个样本。这选择好了的 $N$ 个样本用来训练一棵决策树,作为决策树根节点处的样本。 2. 当每个样本有 $M$ 个属性时,在决策树的每个节点需要分裂时,随机从这 $M$ 个属性中选取出 $m$ 个属性,满足条件 $m < < M$。然后从这 $m$ 个属性中采用某种策略(比如说信息增益)来选择 1 个属性作为该节点的分裂属性。 3. 决策树形成过程中每个节点都要按照步骤 2 来分裂(很容易理解,如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性,则该节点已经达到了叶子节点,无需继续分裂了)。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。 4. 按照步骤 1~3 建立大量的决策树,这样就构成了随机森林了。 > 1. 为什么要随机抽样训练集? > > 如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的,这样的话完全没有**bagging**的必要了。 > > 2. 为什么要有放回抽样? > > 如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有**交集**的,这样每棵树训练出来都是有很大差异的。而**随机森林最后分类取决于多棵树(弱分类器)的投票表决**,这种表决应该是“**求同**”的。因此使用**完全不同的训练集**来训练每棵树这样对最终分类结果是没有帮助的,这样无异于是“盲人摸象”。 ## 3 如何让随机森林中决策树的结构更有多样性 1. **随机抽取数据集。** 通过 $bootstrap$ 的方法得到不同于 $D$ 的 $D^’$,基于 $D^’$ 构建模型。 2. **随机抽取子特征。** 1. 比如原来 100 个特征,只随机选取 30 个进行构建决策树。这样,每一轮得到的树由不同的 30 个特征构成,每个树不一样。 2. 这种类似 $d$ 到 $d^’$ 维的特征变换,相当于从高维到低维的投影,也就是 $d^’$ 维 $z$ 空间是 $d$ 维 $x$ 空间的一个随机子空间。通常 $d^’$ 远小于 $d$,这样算法才更有效率。 3. 随机森林算法的作者建议在构建 $CART$ 每个分支 $b(x)$ 的时候,都可以重新选择子特征来训练,从而得到更具有多样性的决策树。所以说,这种增强的随机森林算法增加了**随机子空间**(Random Subspace)。 3. **现有特征的线性组合。** 1. 除了随机抽取特征之外,还可以将现有的特征 $x$,通过数组 $p$ 进行线性组合,来保持多样性:$\phi_i(x)=p_i^Tx$。 2. 这种方法使每次分支得到的不再是单一的子特征的集合,而是子特征的线性组合(权重不为 1)。好比在二维平面上不只得到水平线和垂直线,也能得到各种斜线。这种做法使子特征选择更加多样性。 3. 值得注意的是,不同分支 $i$ 下的 $p_i$ 是不同的,而且向量 $p_i$ 中大部分元素为零,因为我们选择的只是一部分特征,这是一种低维映射。 4. 所以,这里的随机森林算法又有增强,由原来的**随机子空间**(Random Subspace)变成了**随机组合**(Random Combination),这里的随机组合类似于**感知器**(Perceptron)模型。 ## 4 如何使用 $OOB$ 来验证组合模型 $G$ 的好坏 1. 首先看一个样本 $(x_n,y_n)$ 是那些 $g_t$ 的 $OOB$ 资料。 2. 然后计算 $(x_n,y_n)$ 在这些 $g_t$ 上的表现。 3. 最后将所有样本的表现求平均即可。 例如,样本 $(x_N,y_N)$ 是 $g_2,g_3,g_T$ 的 $OOB$,则可以计算 $(x_N,y_N)$ 在 $G_N^-(x)$ 上的表现为: $$ G_N^-(x)=average(g_2,g_3,g_T) $$ 则所有样本的平均表现为: $$ E_{oob}(G)=\frac1N\sum_{n=1}^Nerr(y_n,G_N^-(x_n)) $$ **$E_{obb}$ 估算的就是 $G$ 的表现好坏**,我们把 $E_{obb}$ 称为**bagging**或**随机森林**的**自我验证**(Slef Validation)。这种自我验证相比于**验证**(Validation)来说还有一个优点就是他不需要重复训练。 1. 如下图左边所示,在通过 $D_{val}$ 选择到表现最好的 $g_{m^*}$ 之后,还需要在 $D_{train}$ 和 $D_{val}$ 组成的所有样本集 $D$ 上重新对该模型 $g_{m^*}$ 训练一次,以得到最终的模型系数。 2. 但是自我验证在调整随机森林算法相关系数并得到最小的 $E_{oob}$ 之后,就完成了整个模型的建立,无需重新训练模型。在随机森林算法中,自我验证在衡量 $G$ 的表现上通常相当准确。 ## 5 特征选择 ### 5.1 含义 如果样本资料特征过多(假如有 10000 个特征,而我们只想从中选取 300 个特征),这时候就需要舍弃部分特征。通常来说,需要移除的特征分为两类: 1. **冗余特征**,即特征出现重复。例如年龄和生日。 2. **不相关特征**。例如疾病预测的时候引入的“保险状况”。 这种从 $d$ 维特征到 $d^’$ 维特征的**子集变换**(Subset Transform)$\phi(x)$ 称为**特征选择**(Feature Selection),最终使用这些 $d^’$ 维的特征进行模型训练。 ### 5.2 方法 在对多维特征进行筛选时,可以通过计算每个特征的重要性(即权重),然后再根据重要性的排序进行选择即可。 #### 5.2.1 线性模型 上面的方法在线性模型中比较容易计算。因为线性模型的 $score$ 是由每个特征经过加权求和而得到的,而加权系数的绝对值 $\omega_i$ 正好代表了对应特征 $x_i$ 的重要性为多少,$\omega_i$ 越大,表示对应特征 $x_i$ 越重要,则该特征应该被选择。$\omega$ 的值可以通过对已有的数据集 $(x_i,y_i)$ 建立线性模型而得到。 #### 5.2.2 非线性模型 对于非线性模型来说,因为不同特征可能是非线性交叉在一起的,所以计算每个特征的重要性就变得比较复杂和困难。例如随机森林算法就是一个非线性模型,接下来我们将讨论如何在随机森林下进行特征选择。 ##### 5.2.2.1 随机测试 ###### 5.2.2.1.1 含义 随机森林中,特征选择的核心思想是**随机测试**(Random Test),随机测试的做法是: 1. 对于某个特征,如果用另外一个随机值替代它之后的表现比之前更差,则表明该特征比较重要,所占的比重应该较大,不能用一个随机值替代。 2. 相反,如果随机值替代后的表现没有太大差别,则表明该特征不那么重要,可有可无。 所以,通过比较某特征被随机值替代前后的表现,就能推断出该特征的权重和重要性。 ###### 5.2.2.1.2 随机值选择方法 **随机测试**的随机值的选择方法有两种,具体如下: 1. 使用**均匀**(Uniform)或者**高斯分布**(Gaussian)抽取随机值替换特征。 2. 通过**排列**(Permutation)的方式将原来的所有 $N$ 个样本的第 $i$ 个特征值重新打乱分布(相当于重新洗牌)。 相比较而言,第二种方法更为科学,因为他保证了特征替代值与原特征的分布是近似的(只是重新洗牌而已),这种方法叫做**随机序列测试**(Permutation Test),即在计算第 $i$ 个特征重要性的时候,将 $N$ 个样本的第 $i$ 个特征重新洗牌,然后比较 $D$ 和 $D^{(p)}$ 表现形式的差异。如果差异很大,则表明第 $i$ 个特征是重要的。 ###### 5.2.2.1.3 衡量替换前后的表现的方法 * 替换前后的表现可以用 $E_{oob}(G)$ 来衡量,但是,对于 $N$ 个样本的第 $i$ 个特征值重新洗牌重置的 $D^{(p)}$,要对他进行重新训练,而且每个特征值都要重复训练,然后再与原 $D$ 的表现进行比较,过程非常繁琐。 * 为了简化运算,随机森林的作者提出了一种方法,就是把**排列**的操作从原来的 $training$ 上移到了 $OOB \space Validation$ 上去,记为 $E_{oob}(G^{(p)}) \rightarrow E_{oob}^{(p)}(G)$。 * 也就是说,在训练的时候仍然使用 $D$,但是在 $OOB$ 验证的时候,将所有的 $OOB$ 样本的第 $i$ 个特征重新洗牌,验证 $G$ 的表现。这种做法大大简化了计算复杂度,在随机森林的特征选择中应用广泛。 ### 5.3 特征选择的优缺点 #### 5.3.1 优点 1. 提高效率,特征越少,模型越简单。 2. 正则化,防止模型过多出现过拟合。 3. 去除无关特征,保留相关性大的特征,解释性强。 #### 5.3.2 缺点 1. 筛选特征的计算量较大。 2. 不同特征组合,也容易发生过拟合。 3. 容易选到无关特征,解释性差。 ## 6 随机森林算法的优点 随机森林算法的优点主要有三个: 1. 不同决策树可以由不同主机并行训练生成,效率很高。 2. 随机森林算法继承了 $CART$ 算法的优点。 3. 将所有的决策树通过 $bagging$ 的形式结合起来,避免了单个决策树造成过拟合的问题。 ## 7 参考文献 1. [随机森林 – Random forest](https://easyai.tech/ai-definition/random-forest)。 2. [随机森林算法及其实现(Random Forest)](https://blog.csdn.net/yangyin007/article/details/82385967)。 3. [随机森林](https://tsinghua-gongjing.github.io/posts/random_forest.html)。 4. [10 -- Random Forest](https://github.com/apachecn/ntu-hsuantienlin-ml/blob/master/28.md)。
ricear
2021年4月6日 15:37
©
BY-NC-ND(4.0)
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
分享
链接
类型
密码
更新密码