💻 Computer Basics
1、计算机网络
1.1 传输层:TCP和UDP
1.1.1 三次握手
1.1.2 四次挥手
1.1.3 流量控制
1.1.4 拥塞控制
1.1.5 TCP和UDP的区别
1.1.6 TCP如何保证传输的可靠性
1.1.7 TCP长连接和短连接
1.1.8 应用层提高UDP协议可靠性的方法
1.1.9 UDP和IP的首部结构
1.2 应用层:HTTP和HTTPS
1.2.1 HTTP和HTTPS的区别
1.2.2 GET和POST的区别
1.2.3 Session与Cookie的区别
1.2.4 从输入网址到获得页面的过程(越详细越好)
1.2.5 HTTP请求有哪些常见的状态码
1.2.6 什么是RIP,算法是什么
1.2.7 HTTP1.1和HTTP2.0的主要区别
1.2.8 DNS
1.2.9 HTTPS加密和认证过程
1.2.10 常见网络攻击
1.2.11 REST
1.3 计算机网络体系结构
1.4 网络层协议
1.4.1 IP地址的分类
1.4.2 划分子网
1.4.3 什么是ARP协议
1.4.4 NAT协议
2、操作系统
2.1 进程和线程
2.1.1 进程和线程的区别
2.1.2 进程间通信方式
2.1.3 同步原语
2.1.4 进程状态
2.1.5 进程调度策略
2.1.6 僵尸进程和孤儿进程
2.1.7 协程
2.1.8 异常控制流
2.1.9 IO多路复用
2.1.10 用户态和内核态
2.2 死锁
2.3 内存管理
2.3.1 分段与分页
2.3.2 虚拟内存
2.3.3 页面置换算法
2.3.4 局部性原理
2.3.5 缓冲区溢出
2.4 磁盘调度
-
+
游客
注册
登录
应用层提高UDP协议可靠性的方法
TCP 协议的重传机制对实时音视频传输而言,如果**网络质量很差**、**丢包率很高**,**重传机制导致传输延迟急剧增加**,**传输质量严重下滑**,因此**实时音视频传输协议一般采用 UDP**(**应用层基于 UDP 的 RTP 协议**,**为视频传输提供序号和音视频同步服务**),UDP 具有**高吞吐**和**低延迟**的特点,然而,基于 UDP 的 RTP 传输在复杂的公网环境下,会时常面临**丢包**、**乱序**、**重复**、**抖动**等问题,严重影响实时音视频的传输效果,针对这一问题,可以采用**前向纠错**(Forward Error Correction, FEC)的方法解决。 ## 1 前向纠错 ### 1.1 含义 1. 前向纠错是一种**在单向通信系统中控制传输错误的技术**,**通过连同数据发送额外的信息进行错误恢复**,**以降低比特误码率**,**发送方将要发送的数据加上一定的冗余纠错码一起发送**,**接收方则根据纠错码**(Error Correcting Code, ECC)**对接收到的数据进行差错检测**,**如发现差错**,**则由接收方进行纠错**。 ### 1.2 常用纠错码 1. 纠错码是**在传输过程中发生错误后能在接收端自行发现并纠正错误的码**,**为了使一种码具有检错或纠错能力**,**需对原码字增加多余的码元**,**以扩大码字之间的差别**,**即把原码字按某种规则变成有一定剩余度的码字**,**并使每个码字的码之间有一定的关系**,**关系的建立称为编码**,**码字到达接收端后**,**可以根据编码规则是否满足来判定有无错误**,**当不能满足时**,**按照一定规则确定错误所在位置并予以纠正**,**纠错并恢复原码字的过程称为译码**。 2. 常见的纠错码有**汉明码**、**BCH 码**、**RS 码**等。 #### 1.2.1 汉明码 ##### 1.2.1.1 含义 1. 汉明码也称作「**海明码**」,英文名为 Hanming Code,在通信领域中,汉明码有广泛的应用,由[理查德·卫斯里·汉明](https://zh.wikipedia.org/wiki/%E7%90%86%E6%9F%A5%E5%BE%B7%C2%B7%E8%A1%9B%E6%96%AF%E9%87%8C%C2%B7%E6%BC%A2%E6%98%8E)于 1950 年发明,是一种「**错误纠正码**」,可以用来**检测并且纠正数据从发送端发往接收端中发生的错误**。 2. 汉明码的发明者[理查德汉明](https://zh.wikipedia.org/wiki/%E7%90%86%E6%9F%A5%E5%BE%B7%C2%B7%E8%A1%9B%E6%96%AF%E9%87%8C%C2%B7%E6%BC%A2%E6%98%8E)在 1940 年代晚期,运用[贝尔模型 V](https://zh.wikipedia.org/w/index.php?title=%E8%B2%9D%E7%88%BE%E6%A8%A1%E5%9E%8BV&action=edit&redlink=1)(Bell Model V)电脑于贝尔实验室工作,输入端是依靠打孔卡,这不免会造成些读取错误,在工作日,当机器检测到错误将停止并闪灯,使得操作员能够解决这个错误,在周末和下班期间,没有操作者的情况下,机器只会简单地转移到下一个工作。 3. 汉明在周末工作,他对于不可靠的读卡机发生错误后,总是不得不重新启动程序变得愈来愈沮丧,在接下来的几年中,他为了解决侦错的问题,开发了功能日益强大的侦错算法,在 1950 年,他发表了今日所称的汉明码,并且时至今日仍在修正错误存储器(Error-Correcting Code Memory)上显示其应用价值。 ##### 1.2.1.2 什么是冗余位 1. 冗余位是一种二进制位,他**被用来添加到需要传输的数据信息中**,**以确保信息在传输过程中不会发生丢失或者改变**。 2. 对于冗余位究竟**需要多少位**这个问题,可以用如下公式来计算: $$ 2^r \ge m + r + 1 $$ 其中,$r$ 指的是**冗余位究竟需要多少位**,而 $m$ 指的是**传输的数据的二进制位数**,假设传输的数据的二进制位数是 7 位,那么冗余位的个数就可以通过上面的公式来计算: $$ 2^4 ≥ 7 + 4 + 1 $$ 因此,我们至少需要 4 个二进制位作为冗余位。 ##### 1.2.1.3 奇偶校验位 1. 一个奇偶校验位是用来**添加至二进制数据中的比特位**,他**通过确保整个二进制数据信息中 1 的个数是奇数还是偶数**,**来判断数据是否在传输过程中发生改变**,因此,存在两种类型的检测方式: 1. **奇校验**: 1. 在奇校验检测方式中,对于**需要发送的数据信息比特**,**检查其中的 1 的个数**,**如果这串比特中 1 的个数是奇数**,**为了保证加上冗余位后**,**整串数据中 1 的个数最后为奇数**,**冗余位上应该设置为 0**,**如果在没有添加冗余位之前**,**数据比特流中的 1 的个数为偶数**,**那么为了最后把 1 的个数凑成一个奇数**,**冗余位上应该设置为 1**。 2. **偶校验**: 1. 同理,在偶校验检测方式中,对于**需要发送的数据信息比特**,**仍然检查其中 1 的个数**,**如果这串比特中 1 的个数是奇数**,**为了保证加上冗余位后**,**整串数据中 1 的个数最后为偶数**,**冗余位上应该设置为 1**,**如果在没有添加冗余位之前**,**数据比特流中的 1 的个数为偶数**,**那么为了最后把 1 的个数凑成一个偶数**,**冗余位上应该设置为 0**。 2. 具体实例如下: 1. 本次我们使用偶校验来作为演示,即我们需要保证数据二进制位加上奇偶校验位的整个数据中,1 的个数应该为偶数,假设本次需要传送的数据信息为 3 位二进制位,演示动画如下:  2. 正如动画演示的那样,我们的奇偶校验位成功的添加到了需要传递的数据信息中了,本次动画采用的是偶校验的方式,即 1 的个数最后一定要满足是偶数。 3. 现在假设在传输过程中,其中 1 位数字发生了改变,演示动画如下:  4. 此时,偶校验电路发现最后 1 的个数不是偶数了,说明在数据传输过程中肯定发生了改变,然而,奇偶校验法仍然存在下面两条缺点: 1. 虽然**知道数据在传输过程中发生了改变**,但并**不知道是哪一位发生了改变**,因而**无法纠正错误**,**只能要求发送方重新发送一遍数据**。 2. 奇偶校验法**只能发现** 1 位、3 位、5 位......等**奇数个二进制位发生改变**,假设数据传送过程中有 2 位发生改变,则奇偶校验法并不能发现数据已经被更改了,仍然认为数据是无误的,如下面的动画所示:  ##### 1.2.1.4 原理 1. 我们上面讲述了「奇偶校验法」的两个缺点,其中一个是当传输过程中发生了 2 位或更大的偶数位改变时,奇偶校验法将会变得失效。 2. 然而,随着科学技术的飞速发展,如今在数据通信传输过程中,数据发生改变的几率是非常小的,1 位数据发生改变的几率更加小,因此,2 位及 2 位以上比特位发生改变的情况我们假设其永远不可能发生,因此,我们剩下需要解决的问题就是**假设有 1 位发生改变**,**有没有什么办法能够让我们发现是哪一位发生了改变呢**,**如果能找到是哪一位发生了改变**,**我们就能够纠正他**,**0 变 1**,**1 变 0**,汉明码就很好的解决了这个问题。 3. 汉明码其实就是「**奇偶校验法**」**的升级版**,他是**多个**「**奇偶校验法**」**的组合糅合在一起**,但是**奇偶校验位的位置不一定再是最后一位了**,**而是有其他的计算方法**。 4. 假设我们需要**传输的数据信息是由 7 位二进制位组成**,通过[什么是冗余位](https://notebook.ricear.com/project-26/doc-929/#1-2-1-2-%E4%BB%80%E4%B9%88%E6%98%AF%E5%86%97%E4%BD%99%E4%BD%8D)我们已经算出来了**至少需要 4 位冗余位**,因此,**整个信息流有 11 个二进制位**,其中有**7 位数据位**和**4 位奇偶校验位**。 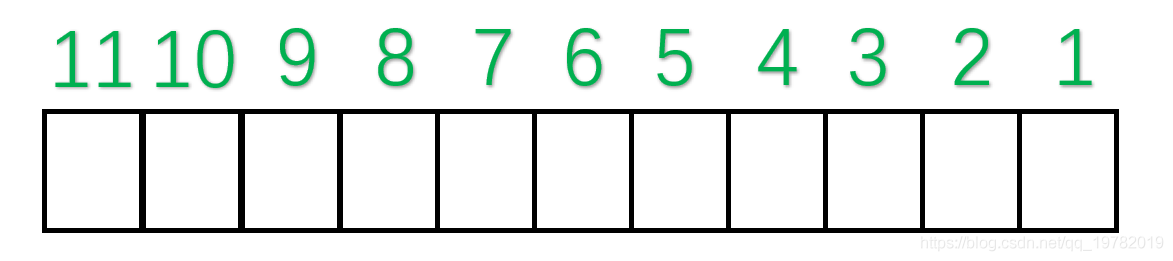 5. 汉明码对于奇偶校验位的位置有特殊的规定,**所有 2 的幂次位作为奇偶校验位**,因此,**第 1 位**、**第 2 位**、**第 4 位**、**第 8 位为奇偶校验位**,**其他的 7 位为数据位**。  6. 我们把索引用二进制表示,如下图所示: 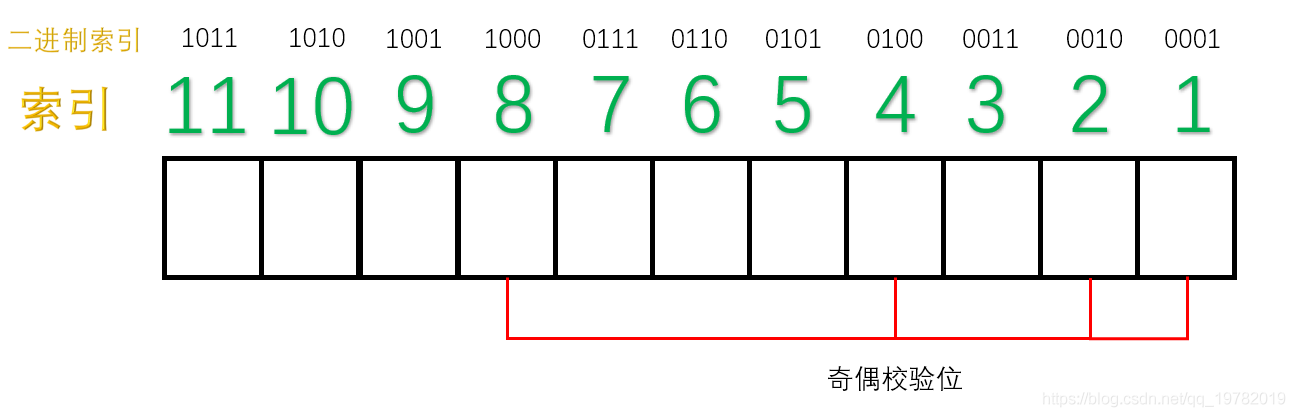 7. 接下来对二进制索引通过以下方式进行分类: 1. **从低位往高位数**,**第一位是 1 的索引有 0001**、**0011**、**0101**、**0111**、**1001**、**1011**,**对应的十进制为 1**、**3**、**5**、**7**、**9**、**11**,那么**这几位上面的数据位和 1 号奇偶校验位构成了一组**。 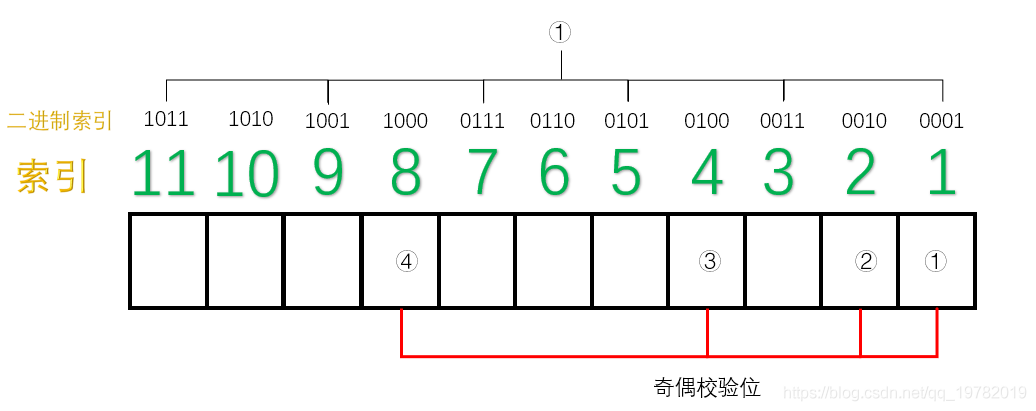 2. 同理,**从低位往高位数**,**第二位是 1 的索引有 0010**、**0011**、**0110**、**0111**、**1010**、**1011**,**对应的十进制为 2**、**3**、**6**、**7**、**10**、**11**,那么**这几位上面的数据位和 2 号奇偶校验位构成了一组**。 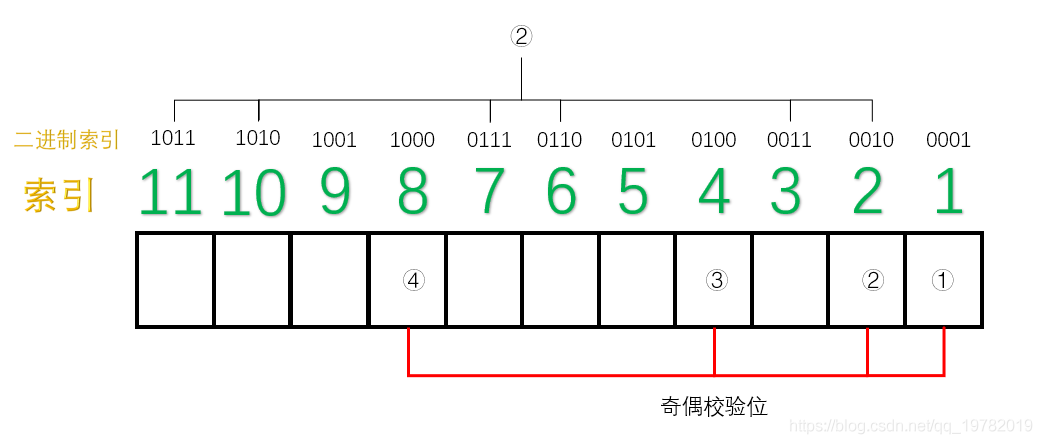 3. 同理,**3 号奇偶校验位和 4 号奇偶校验位管理的数据位分别如下**:  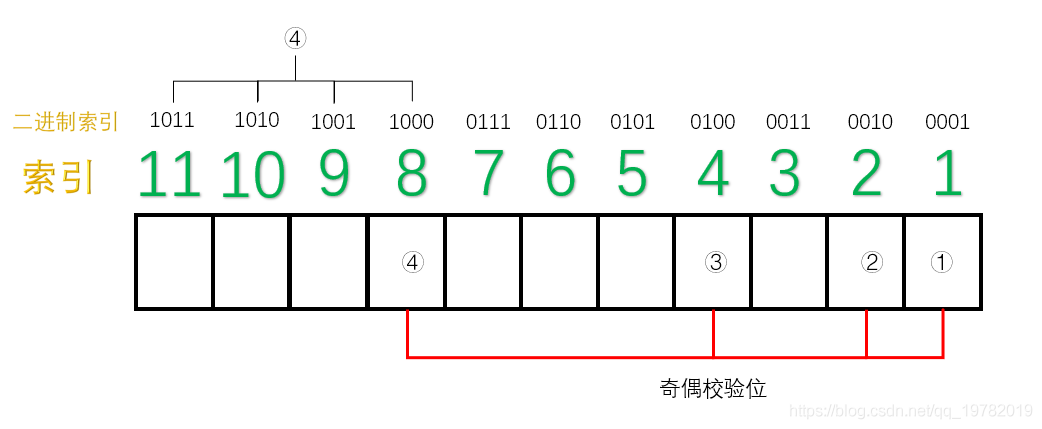 8. 这样,**分组我们就已经确立好了**,接下来需要开始**填充数据位**,假设我们需要传输的 7 位数据位为 1011001。 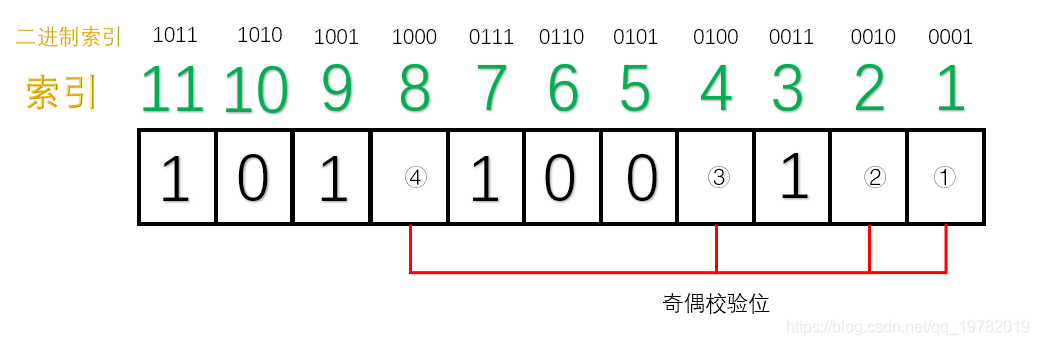 9. 接下来,我们就需要**分别填充每一组的奇偶校验位**了(采用**奇校验**): 1. 对于**第一组**来说,**数据位上 1 的个数为 4 个**,**偶数个**,因此**① 号应该为 1**,这样**第一组数据位上 1 的个数最后才能保证为奇数**。 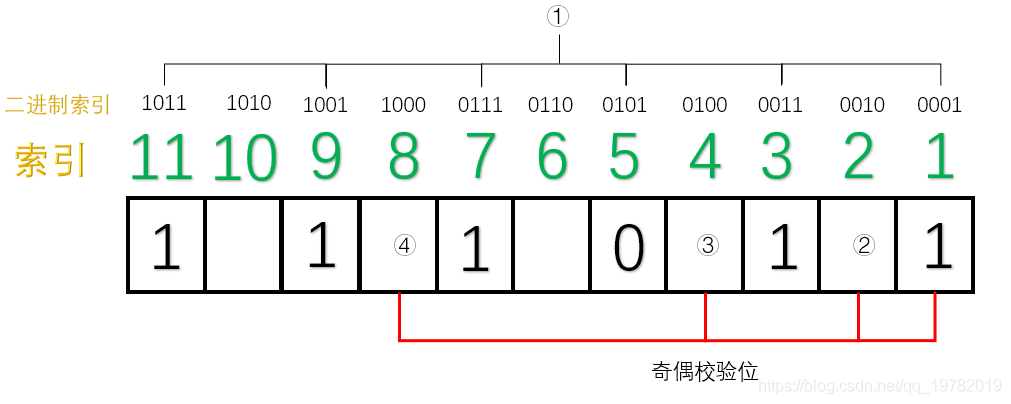 2. 同理,对于**第二组**来说,**数据位上 1 的个数为 3 个**,**已经是奇数了**,因此**② 号应该是 0**,这样**第二组数据位上 1 的个数最后才能保证为奇数**。 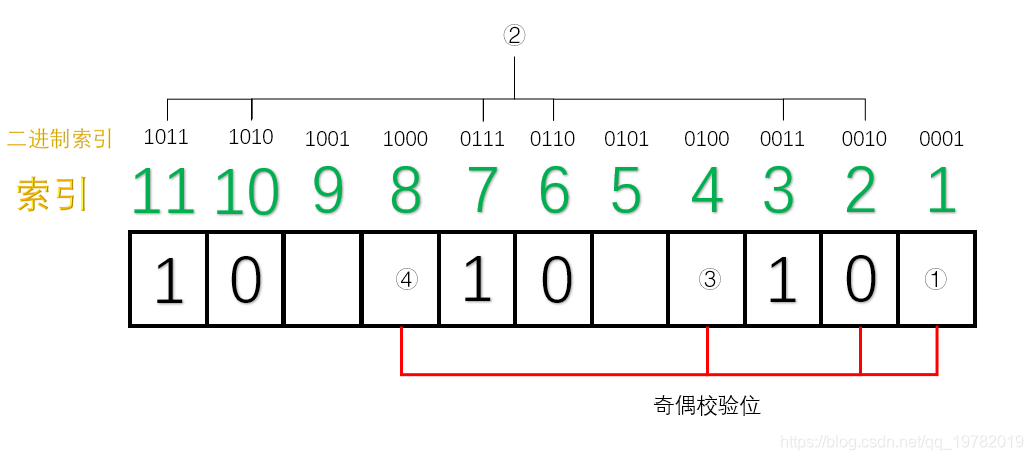 3. 对于**第三组**来说,**数据位上 1 的个数为 1 个**,因此**③ 号应该是 0**。 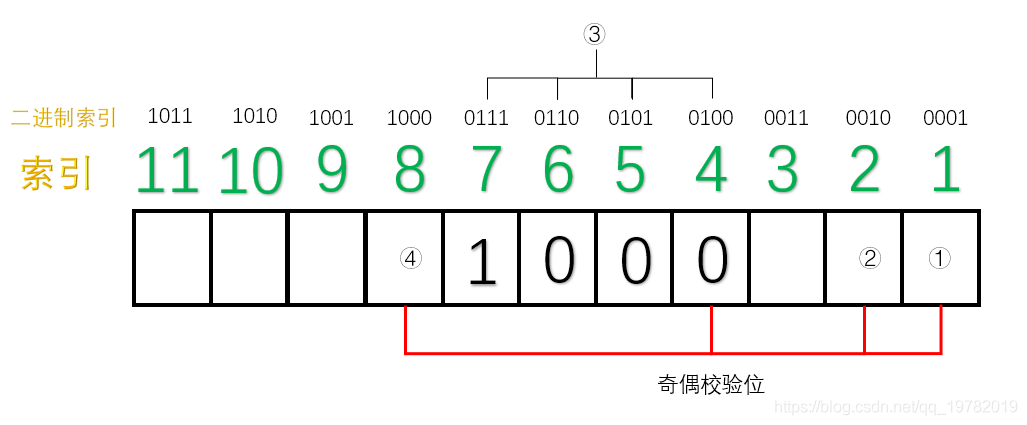 4. 对于**第四组**来说,**数据位上 1 的个数为 2 个**,因此**③ 号应该是 1**。 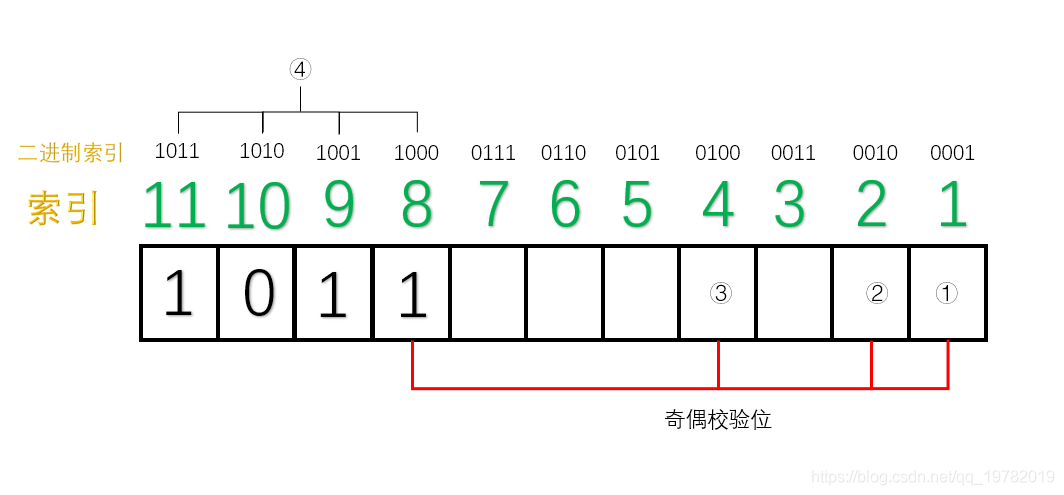 10. 最后,总的汉明码就构造完毕了,如下图所示: 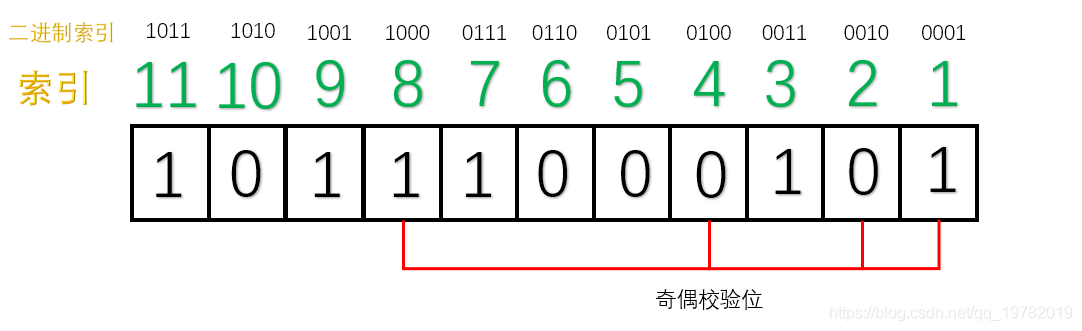 ##### 1.2.1.5 纠错和改正 1. 上面我们已经完成了汉明码的编码,下面我们将阐述汉明码是如何发现错误以及改正错误的。 2. 假设**第 5 号位上的 0 在传输过程中变成了 1**,**接收方收到的数据则为 10111010101**。 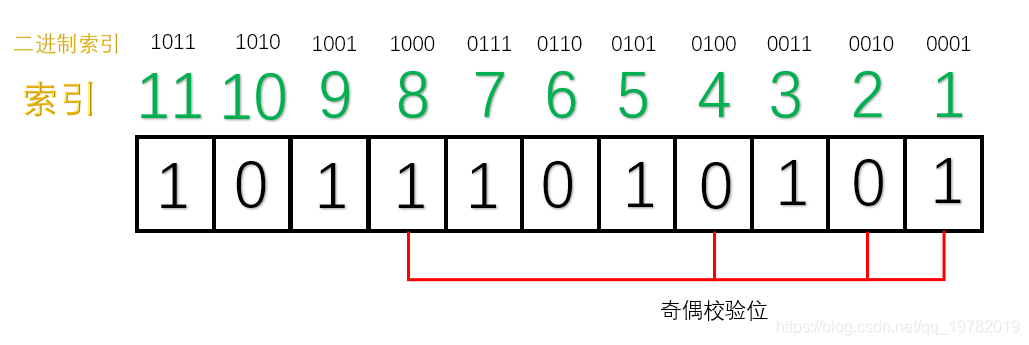 3. 汉明码**通过检查每一小组的奇校验来确定是否发生了错误**: 1. 首先**第一组**,**数据位上 1 的个数为 6 个**,**不再是奇数个了**,因此我们可以断定**这一组中肯定有某个数据发生了错误**,**但不能确定是哪一位上发生了错误**,**为了达到奇校验**,**我们必须补 1 个 1 来达到奇数个**。 2. 接下来我们检查**第二组**,**数据位上 1 的个数为 3 个**,**仍然满足奇校验**,因此我们也可以断定**这一组中没有任何一位数据发生了改变**,所以我们只需要**补个 0**。 3. 我们继续检查**第三组**,**数据位上 1 的个数为 2 个**,**不再满足奇校验,因此我们可以断定这一组中也有数据发生改变**,**为了达到奇校验**,**我们必须补 1 个 1 来达到奇数个**。 4. 我们继续检查**第四组**,**数据位上 1 的个数为 3 个**,**满足奇校验**,因此**没有发生改变**,所以我们只需要**补个 0**。 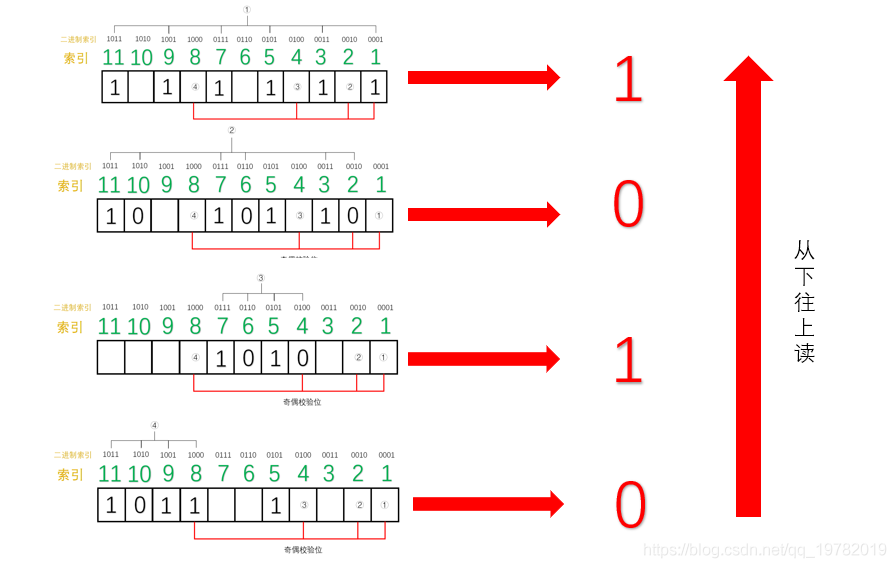 4. 我们发现**最后得出来的二进制数是 0101**,我们会神奇地发现**0101 就是对应的十进制为 5**,因此我们可以准确的知道**5 号位上发生了数据的改变**,我们**只需要对 5 号位进行置反操作即可**,最后,**接收方就可以修改为正确的数据啦**。 ## 参考文献 1. [【实时音视频传输/流媒体通信】FEC 前向纠错的原理和实现](https://blog.csdn.net/Xinyue_Lu/article/details/109165717?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~aggregatepage~first_rank_ecpm_v1~rank_v31_ecpm-5-109165717-null-null.pc_agg_new_rank&utm_term=udp%E5%89%8D%E5%90%91%E7%BA%A0%E9%94%99&spm=1000.2123.3001.4430)。 2. [纠错技术之 FEC(向前纠错)](https://www.cnblogs.com/cainiao-chuanqi/p/12107314.html)。 3. [汉明码——计算机网络——全网最通俗的讲解](https://blog.csdn.net/qq_19782019/article/details/87452394)。
ricear
2022年6月18日 21:22
©
BY-NC-ND(4.0)
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
分享
链接
类型
密码
更新密码