🧮 Algorithm Notebook
1、算法准备
1.1 牛客网编程OJ的典型输入输出
2、算法框架
2.1 动态规划
2.1.1 斐波那契数列
2.1.2 背包问题
2.1.3 贪心算法
2.1.4 序列和数组类问题
2.1.5 编辑距离
2.1.6 高楼扔鸡蛋
2.1.7 股票问题系列通解
2.1.8 最长有效括号
2.1.9 剪绳子
2.1.10 正则表达式匹配
2.2 二分查找
2.2.1 二分查找框架
2.2.2 搜索旋转排序数组
2.3 链表
2.3.1 反转链表
2.3.2 相交链表
2.3.3 合并链表
2.3.4 链表中倒数第k个节点
2.3.5 复制带随机指针的链表
2.4 排序算法
2.4.1 常见排序算法
2.5 二叉树
2.5.1 二叉树遍历
2.5.2 岛屿问题
2.5.3 二叉树路径问题
2.5.4 构造二叉树
2.6 回溯算法
2.6.1 回溯算法解题框架
2.6.2 N皇后
2.7 数组
2.7.1 删除有序数组中的重复项
2.7.2 滑动窗口最大值
2.7.3 调整数组顺序使奇数位于偶数前面
2.7.4 螺旋矩阵
2.7.5 多数元素
2.7.6 最大数
2.7.7 和为s的两个数字
2.7.8 构建乘积数组
2.7.9 两数之和
2.8 字符串
2.8.1 最小覆盖子串
2.8.2 比较版本号
2.8.3 验证IP地址
2.8.4 基本计算器 II
2.8.5 字符串解码
2.8.6 移掉 K 位数字
2.8.7 无重复字符的最长子串
2.8.8 第一个只出现一次的字符
2.8.9 翻转字符串里的单词
2.8.10 字符串转换整数 (atoi)
2.8.11 字符串四则运算
2.9 栈
2.9.1 最小栈
2.9.2 弹出序列
2.10 数学
2.10.1 用 Rand7() 实现 Rand10()
2.10.2 只出现一次的数字
2.10.3 整数反转
2.10.4 求1+2+…+n
2.10.5 二进制中1的个数
2.10.6 幂运算
2.10.7 1~n 整数中 1 出现的次数
2.10.8 数字序列中某一位的数字
2.10.9 丑数
2.10.10 n个骰子的点数
2.10.11 圆圈中最后剩下的数字
2.10.12 不用加减乘除做加法
2.10.13 x 的平方根
2.11 设计
2.11.1 LRU 缓存机制
-
+
游客
注册
登录
搜索旋转排序数组
## 1 题目 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。 给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。 **示例 1:** ```txt 输入:nums = [4,5,6,7,0,1,2], target = 0 输出:4 ``` **示例 2:** ```txt 输入:nums = [4,5,6,7,0,1,2], target = 3 输出:-1 ``` **示例 3:** ```txt 输入:nums = [1], target = 0 输出:-1 ``` **提示:** * 1 <= nums.length <= 5000 * -10^4 <= nums[i] <= 10^4 * nums 中的每个值都 独一无二 * 题目数据保证 nums 在预先未知的某个下标上进行了旋转 * -10^4 <= target <= 10^4 **进阶:** 你可以设计一个时间复杂度为 O(log n) 的解决方案吗? ## 2 解题思路 ### 2.1 两段寻找 #### 2.1.1 问题分析 1. 这种方法的基本思想是**将数组分成两部分**,分别是**前面一部分的升序数组**和**后面一部分的升序数组**。 2. 首先**对前面一部分的升序数组进行遍历**,**找到两部分数组的边界**,在遍历的过程中,如果**找到了目标元素**,那么**直接返回对应的下标**即可。 3. 如果**前一部分没有找到目标元素**,并且**已经找到了两部分数组的边界**,此时直接**对后面一部分的数组进行二分查找**即可。 #### 2.1.2 参考代码 ```java /** * 对一个数组指定范围内的数据二分查找目标数据 * * @param nums 数组 * @param target 目标元素 * @return 目标元素在数组中的位置 */ public int binarySearch(int[] nums, int start, int end, int target) { int left = start, right = end; while (left <= right) { int mid = left + (right - left) / 2; if (nums[mid] < target) { left = mid + 1; } else if (nums[mid] > target) { right = mid - 1; } else if (nums[mid] == target) { return mid; } } return -1; } /** * 33. 搜索旋转排序数组(版本 1:两段寻找) * * @param nums 数组 * @param target 目标元素 * @return 目标元素在数组中的位置 */ public int searchV1(int[] nums, int target) { int len = nums.length; // 用于后面判断数组第一阶段升序范围 int start = nums[0]; int end = -1; if (start == target) {return 0;} // 首先判断数组的第一阶段升序范围,如果在这一范围内找到目标元素,则直接返回相应的下标 for (int i = 1; i < len; i++) { if (nums[i] == target) {return i;} if (nums[i] < start) { end = i; break; } start = nums[i]; } // 如果在数组第一阶段升序范围没有找到目标元素,则在后面一阶段升序范围采用二分查找法查找目标元素 return end == -1 ? -1 : binarySearch(nums, end, len - 1, target); } ``` ### 2.2 二分查找 #### 2.2.1 问题分析 1. 这种方法的基本思想是**直接在原来的数组上进行二分查找**,但是由于**基本的二分查找算法只能用于升序数组上**,因此**需要对基本的二分查找算法进行改进**。 2. 主要改进的地方在于在遍历的过程中**先判断 $nums[mid]$ 位于左段还是右段**: 1. 如果 $nums[mid] \ge nums[left]$,说明 $nums[mid]$ 位于**左段**,然后再**判断 $target$ 的位置**: 1. 如果 $target \ge nums[left]$ 并且 $target \lt nums[mid]$,说明 $target$ 位于 $nums[mid]$**左边**,则 $right = mid - 1$。  2. 否则,说明 $target$ 位于 $mid$**右边**,则 $left = mid + 1$。  2. 如果 $nums[mid] \le nums[right]$,说明 $nums[mid]$ 位于**右段**,然后再**判断 $target$ 的位置**: 1. 如果 $target \gt nums[mid]$ 并且 $target \le nums[right]$,说明 $target$ 位于 $nums[mid]$**右边**,则 $left = mid + 1$。  2. 否则,说明 $target$ 位于 $mid$**左边**,则 $right = mid - 1$。 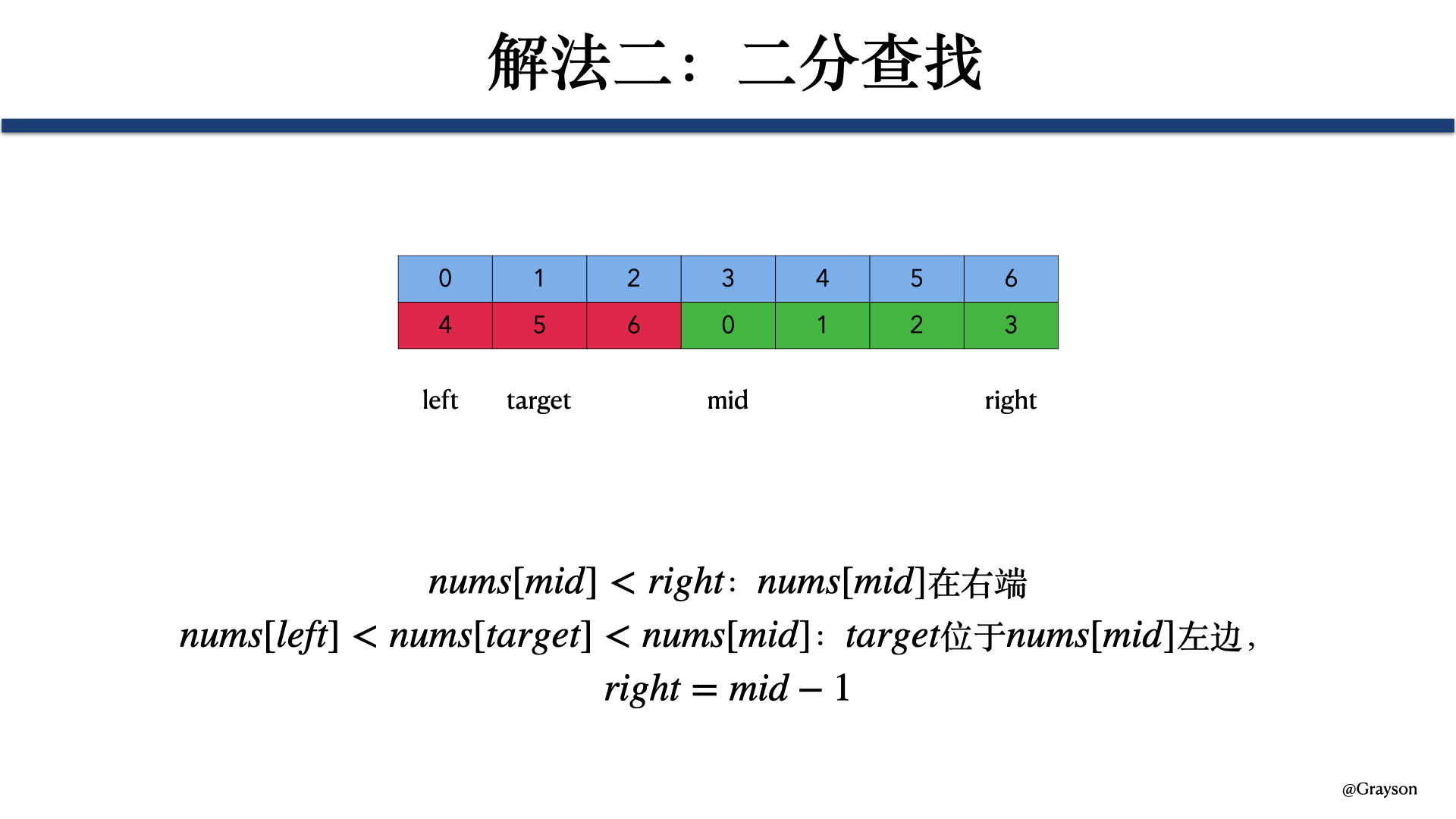 #### 2.2.2 参考代码 ```java /** * 33. 搜索旋转排序数组(版本 2:二分查找) * * @param nums 数组 * @param target 目标元素 * @return 目标元素在数组中的位置 */ public int searchV2(int[] nums, int target) { int left = 0, right = nums.length - 1; while (left <= right) { int mid = left + (right - left) / 2; if (nums[mid] == target) { return mid; } // 判断 nums[mid] 位于左段还是右段 if (nums[mid] >= nums[left]) { // nums[mid] 位于左段 if (target >= nums[left] && target < nums[mid]) { right = mid - 1; } else { left = mid + 1; } } else if (nums[mid] <= nums[right]) { // nums[mid] 位于右段 if (target > nums[mid] && target <= nums[right]) { left = mid + 1; } else { right = mid - 1; } } } return -1; } ``` ## 3 参考文献 1. [33. 搜索旋转排序数组](https://leetcode-cn.com/problems/search-in-rotated-sorted-array)。 2. [多思路完全攻略,🤷♀️ 必须秒懂!](https://leetcode-cn.com/problems/search-in-rotated-sorted-array/solution/duo-si-lu-wan-quan-gong-lue-bi-xu-miao-dong-by-swe)
ricear
2021年8月5日 20:06
©
BY-NC-ND(4.0)
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
分享
链接
类型
密码
更新密码