二叉树遍历

## 算法模板

二叉树遍历算法分为两种，一种是**深度优先遍历算法**，例如前序遍历、中序遍历、后序遍历，另一种是**广度优先遍历算法**，例如层序遍历。

> **创建二叉树**：
>
> ~~~java
> /**
>  * 创建二叉树
>  * @param arr   数组
>  * @param index 元素下标
>  */
> public static TreeNode creatBinaryTree(int[] arr, int index) {
>     TreeNode node = null;
>     if (index < arr.length) {
>         node = new TreeNode(arr[index]);    //  父节点下标为 index
>         node.left = creatBinaryTree(arr, 2 * index + 1);    //  左节点的下标 left 等于 index * 2 + 1
>         node.right = creatBinaryTree(arr, 2 * index + 2);   //  右节点的下标 left 等于 index * 2 + 2
>     }
>     return node;
> }
> ~~~
>
>

### 深度优先遍历算法

#### 递归解法

##### 前序遍历

```java
/**
 * 前序遍历（递归解法）
 *
 * @param head 头结点
 */
public void preOrderRecur(TreeNode head) {
    //  base case
    if (head == null) {
        return;
    }
    //  访问根节点
    System.out.println(head.val);
    //  遍历左节点
    preOrderRecur(head.left);
    //  遍历右节点
    preOrderRecur(head.right);
}
```

##### 中序遍历

> **二叉搜索树的中序遍历为一个递增序列**。

```java
/**
 * 中序遍历（递归解法）
 *
 * @param head 头结点
 */
public void inOrderRecur(TreeNode head) {
    //  base case
    if (head == null) {
        return;
    }
    //  遍历左节点
    preOrderRecur(head.left);
    //  访问根节点
    System.out.println(head.val);
    //  遍历右节点
    preOrderRecur(head.right);
}
```

##### 后序遍历

```java
/**
 * 后序遍历（递归解法）
 *
 * @param head 头结点
 */
public void postOrderRecur(TreeNode head) {
    //  base case
    if (head == null) {
        return;
    }
    //  遍历左节点
    preOrderRecur(head.left);
    //  遍历右节点
    preOrderRecur(head.right);
    //  访问根节点
    System.out.println(head.val);
}
```

#### 迭代解法

##### 前序遍历

1. 初始时，将根节点入栈。
2. 判断栈是否为空，如果栈不为空：

1. 弹出栈顶元素 $node$，并将 $node.val$ 输出。
   2. 如果 $node$ 的右子树不为空，则将其对应的右子树 $node.right$ 入栈。
   3. 如果 $node$ 的左子树不为空，则将其对应的左子树 $node.right$ 入栈。

![](https://notebook.ricear.com/media/202106/前序遍历（迭代解法）_1623760901.gif)

```java
/**
 * 前序遍历（迭代解法）
 *
 * @param head 头结点
 */
public void preOrderInter(TreeNode head) {
    //  base case
    if (head == null) {
        return;
    }
    //  用来模仿递归解法中的栈
    Stack<TreeNode> stack = new Stack<>();
    //  初始时将头结点入栈
    stack.push(head);
    while (!stack.empty()) {
        //  访问根节点
        TreeNode node = stack.pop();
        System.out.println(node.val);
        //  将右节点入栈（左节点会先出栈，所以等价于遍历左节点）
        if (node.right != null) {
            stack.push(node.right);
        }
        //  将左节点入栈（右节点会后出栈，所以等价于遍历右节点）
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}
```

##### 中序遍历

1. 令当前指针 $cur=head$。
2. 判断栈和当前 $cur$ 是否为空，如果二者有一个不为空：
   1. 判断当前 $cur$ 是否为空，如果 $cur$ 不为空（**目的是尽量让当前节点的左子树入栈**）：
      1. 将 $cur$ 入栈。
      2. 令 $cur=cur.left$。
      3. 重复步骤 A，直到 $cur$ 为空。
   2. 弹出栈中的节点 $node$，并输出弹出节点的值 $node.val$。
   3. 如果 $node$ 的右子树不为空，则令 $cur=cur.right$。

![](https://notebook.ricear.com/media/202106/中序遍历（迭代解法）_1623761272.gif)

```java
/**
 * 中序遍历（迭代解法）
 *
 * @param head 头结点
 */
public void inOrderInter(TreeNode head) {
    //  base case
    if (head == null) {
        return;
    }
    TreeNode cur = head;
    //  用来模仿递归解法中的栈
    Stack<TreeNode> stack = new Stack<>();
    while (!stack.empty() || cur != null) {
        //  尽可能将这个节点的左子树入栈，相当于访问左子树
        while (cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
        //  相当于访问根节点
        TreeNode node = stack.pop();
        System.out.println(node.val);
        //  相当于访问右节点
        if (node.right != null) {
            cur = node.right;
        }
    }
}
```

##### 后序遍历

后序遍历和先序遍历类似，不过后序遍历是**左子树先入栈**，**右子树后入栈**。

```java
/**
 * 后序遍历（迭代解法）
 *
 * @param head 头结点
 */
public void postOrderInter(TreeNode head) {
    //  base case
    if (head == null) {
        return;
    }
    //  用来模仿递归解法中的栈
    Stack<TreeNode> stack = new Stack<>();
    //  用于将根节点的值入栈
    Stack<Integer> stack2 = new Stack<>();
    //  初始时将头结点入栈
    stack.push(head);
    while (!stack.empty()) {
        //  访问根节点
        TreeNode node = stack.pop();
        //  将根节点的值入栈
        stack2.push(node.val);
        //  将右节点入栈（左节点会先出栈，所以等价于遍历左节点）
        if (node.right != null) {
            stack.push(node.right);
        }
        //  将左节点入栈（右节点会后出栈，所以等价于遍历右节点）
        if (node.left != null) {
            stack.push(node.left);
        }
    }

//  遍历第二个栈中的值
    while (!stack2.isEmpty()) {
        System.out.println(stack2.pop());
    }
}
```

### 广度优先遍历算法

#### 层序遍历

##### 输出一维数组

和前序遍历类似，不过层序遍历采用的是**队列**来存储相应的节点，因此是**左子树先加入队列**，这样在出队时就是**左子树先出对**。

```java
/**
 * 层序遍历（迭代解法，输出一维数组）
 *
 * @param head 头结点
 */
public void levelOrderInterV1(TreeNode head) {
    //  用户保存根节点
    Queue<TreeNode> queue = new ArrayDeque<>();
    //  初始时将根节点加入队列
    queue.add(head);
    while (!queue.isEmpty()) {
        //  将队列中的节点弹出，然后将其值加入到结果中
        TreeNode node = queue.poll();
        System.out.println(node.val);
        if (node.left != null) {
            //  如果左子树非空，则将左子树加入到队列中
            queue.add(node.left);
        }
        if (node.right != null) {
            //  如果右子树非空，则将右子树加入到队列中
            queue.add(node.right);
        }
    }
}
```

##### 输出二维数组

1. 创建结果数组 $res$，
2. 初始时，将根节点加入队列。
3. 判断队列是否为空，如果队列不为空：
   1. 创建临时结果数组 $tempRes$，然后计算队列的大小为 $n$，然后将队列中的元素依次出队：
      1. 弹出队首元素 $node$，并将 $node.val$ 添加到 $tempRes$ 中。
      2. 如果 $node$ 的右子树不为空，则将其对应的右子树 $node.right$ 加入队列。
      3. 如果 $node$ 的左子树不为空，则将其对应的左子树 $node.left$ 加入队列。
   2. 将 $tempRes$ 添加到中 $res$。

![](https://notebook.ricear.com/media/202106/层序遍历（迭代解法：输出二维数组）_1623762105.gif)

```java
/**
 * 层序遍历（迭代解法，输出二维数组）
 *
 * @param head 头结点
 */
public List<List<Integer>> levelOrderInterV2(TreeNode head) {
    List<List<Integer>> res = new ArrayList<>();
    //  如果头结点为空，则直接返回 res
    if (head == null) {return res;}
    //  用户保存根节点
    Queue<TreeNode> queue = new ArrayDeque<>();
    //  初始时将根节点加入队列
    queue.add(head);
    while (!queue.isEmpty()) {
        //  一次性将同一层的节点都遍历一下
        List<Integer> tempRes = new ArrayList<>();
        int n = queue.size();
        for (int i = 0; i < n; i++) {
            //  将队列中的节点弹出，然后将其值加入到结果中
            TreeNode node = queue.poll();
            tempRes.add(node.val);
            if (node.left != null) {
                //  如果左子树非空，则将左子树加入到队列中
                queue.add(node.left);
            }
            if (node.right != null) {
                //  如果右子树非空，则将右子树加入到队列中
                queue.add(node.right);
            }
        }
        //  将当前层的遍历结果添加到最终结果中
        res.add(tempRes);
    }
    return res;
}
```

##### 输出锯齿形二维数组

1. 该方法是在输出二维数组的基础上加上一个当前遍历层数的判断，如果当前遍历的层数为**偶数层**，则将当前的结果进行**反转一下**，然后再添加到最后的结果中，这样便可以实现输出锯齿形二维数组，具体的演示过程可参考前面的[输出二维数组](#2-1-2-输出二维数组)解法。

```java
/**
 * 层序遍历（迭代解法，输出锯齿形二维数组）
 *
 * @param head 头结点
 */
public List<List<Integer>> zigzagLevelOrderInter(TreeNode head) {
    List<List<Integer>> res = new ArrayList<>();
    //  记录当前遍历的层数
    int level = 0;
    //  如果头结点为空，则直接返回 res
    if (head == null) {return res;}
    //  用户保存根节点
    Queue<TreeNode> queue = new ArrayDeque<>();
    //  初始时将根节点加入队列
    queue.add(head);
    //  遍历的层数加 1
    level++;
    while (!queue.isEmpty()) {
        //  一次性将同一层的节点都遍历一下
        List<Integer> tempRes = new ArrayList<>();
        int n = queue.size();
        for (int i = 0; i < n; i++) {
            //  将队列中的节点弹出，然后将其值加入到结果中
            TreeNode node = queue.poll();
            tempRes.add(node.val);
            if (node.left != null) {
                //  如果左子树非空，则将左子树加入到队列中
                queue.add(node.left);
            }
            if (node.right != null) {
                //  如果右子树非空，则将右子树加入到队列中
                queue.add(node.right);
            }
        }
        //  如果遍历的层数是偶数层，则将当前层的结果反转一下，变为从右往左遍历
        if (level % 2 == 0) {
            List<Integer> tempRes2 = new ArrayList<>();
            for (int i = tempRes.size() - 1; i >= 0; i--) {
                tempRes2.add(tempRes.get(i));
            }
            tempRes = tempRes2;
        }
        //  将当前层的遍历结果添加到最终结果中
        res.add(tempRes);
        level++;
    }
    //  遍历的层数加 1
    return res;
}
```

## 典型题目

### 翻转二叉树

> 题目内容详见[226. 翻转二叉树](https://leetcode-cn.com/problems/invert-binary-tree)。

#### 问题分析

1. 这道题目主要有两种解法，分别是**递归**（深度优先遍历）、**迭代**（广度优先遍历），分别套用前面的相应的模板即可。
2. 需要注意的是：
   1. **递归时需要定义一个临时变量来保存左子树的数据**，**然后再进行下面的递归**。
   2. **迭代时直接在原来访问根节点的地方添加节点替换逻辑即可**。

#### 参考代码

##### 递归

```java
/**
 * 226. 翻转二叉树（版本 1：递归）
 * @param root  根节点
 * @return  反转后的二叉树
 */
public TreeNode invertTreeV1(TreeNode root) {
    return dfs(root);
}

/**
 * 递归翻转二叉树
 * @param root  根节点
 * @return  反转后的二叉树
 */
public TreeNode dfs(TreeNode root) {
    if (root == null) {return null;}

//  保留左子树的数据
    TreeNode leftTemp = root.left;
    root.left = dfs(root.right);
    root.right = dfs(leftTemp);

return root;
}
```

##### 迭代

```java
/**
 * 226. 翻转二叉树（版本 2：层序遍历）
 * @param root  根节点
 * @return  反转后的二叉树
 */
public TreeNode invertTreeV2(TreeNode root) {
    if (root == null) {return null;}

Queue<TreeNode> queue = new ArrayDeque<>();

queue.add(root);
    while(!queue.isEmpty()) {
        TreeNode node = queue.poll();

//  交换节点信息
        TreeNode leftTemp = node.left;
        node.left = node.right;
        node.right = leftTemp;

if (node.left != null) {
            queue.add(node.left);
        }
        if (node.right != null) {
            queue.add(node.right);
        }
    }

return root;
}
```

### 对称二叉树

> 题目内容详见[101. 对称二叉树](https://leetcode-cn.com/problems/symmetric-tree)。

#### 问题分析

1. 对于二叉树的题目，一般可通过**递归**和**迭代**两种方法来求解：

1. 递归时一般需先**找出题目中蕴含的递归关系**，然后**确定递归函数的含义**，一般递归采用的都是**深度优先遍历**，**递归算法也是在原有的深度优先遍历算法上的改进**。
   2. 迭代时一般采用的是**广度优先遍历**，**迭代算法也是在原有的广度优先遍历算法上的改进**。

2. **如果一棵树的左子树和右子树对称**，**那么这个树是对称的**。

3. 因此，这个问题可以转化为**两棵树在什么情况下互为镜像**，如果同时满足下面的条件，两棵树互为镜像：

1. 他们的**两个根节点具有相同的值**。
   2. **每个树的左子树都与另一个树的右子树镜像对称**。
   3. **每个树的右子树都与另一个树的左子树镜像对称**。

4. 我们可以实现这样一个递归函数，**通过同步移动两个指针的方法来遍历这棵树**：

1. **$left$ 指针和 $right$ 指针一开始都指向这棵树的根**。
   2. **随后 $left$ 左移时**，$right$**右移**，$left$**右移时**，**$right$ 左移**。
   3. **每次检查当前 $left$ 和 $right$ 节点的值是否相等**，**如果相等再判断左右子树是否对称**。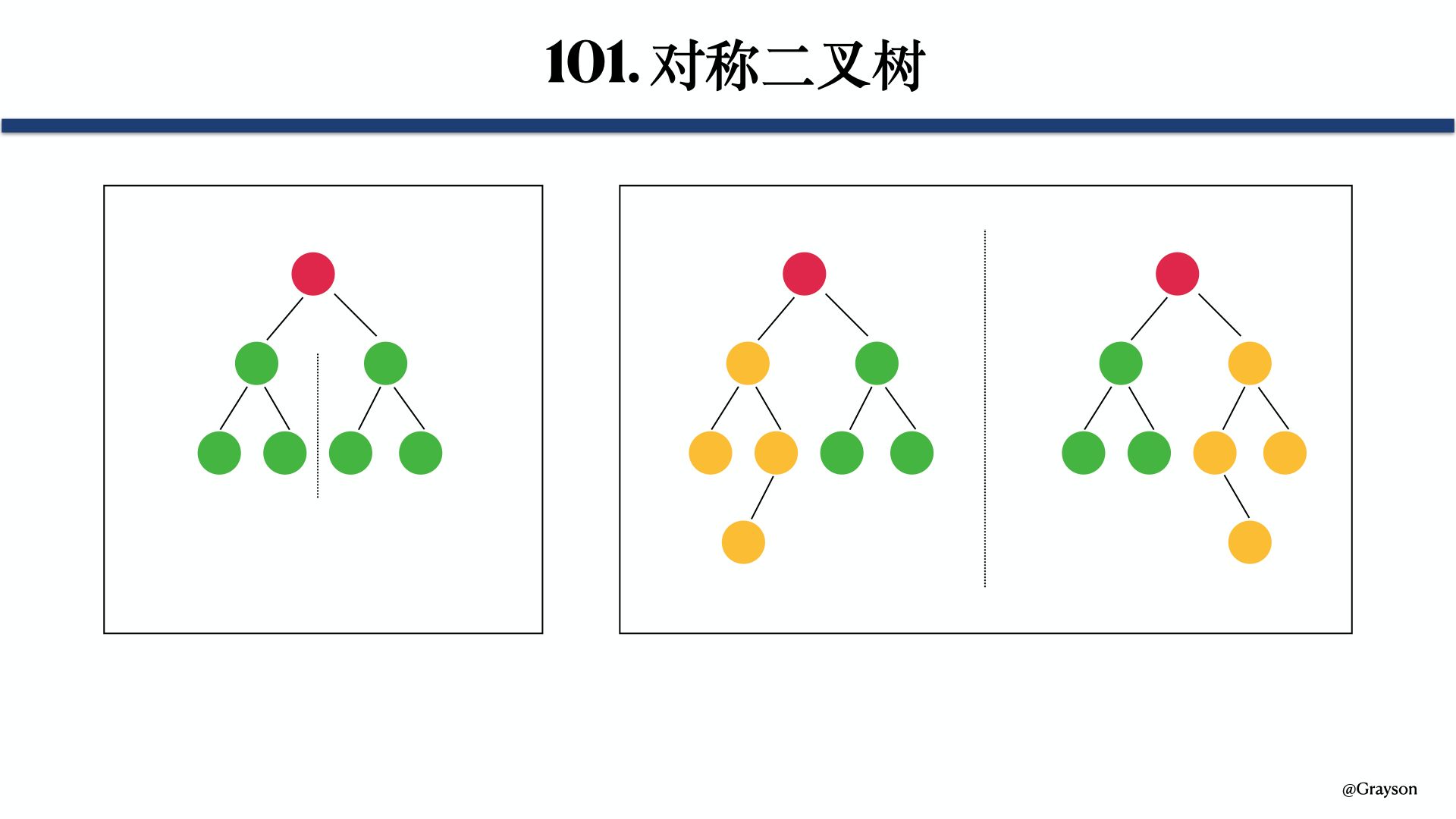

![](https://notebook.ricear.com/media/202108/2021-08-05_223219.png)

#### 参考代码

##### 递归

```java
/**
 * 101. 对称二叉树（版本 1：递归）
 *
 * @param root 根节点
 * @return 二叉树是否镜像对称
 */
public boolean isSymmetricV1(TreeNode root) {
    if (root == null) {return true;}
    return dfs(root.left, root.right);
}

/**
 * 递归判断二叉树是否镜像对称
 *
 * @param left  左子树
 * @param right 右子树
 * @return 二叉树是否镜像对称
 */
public boolean dfs(TreeNode left, TreeNode right) {
    if (left == null && right == null) {return true;}
    if (left == null || right == null) {return false;}
    return left.val == right.val && dfs(left.left, right.right) && dfs(left.right, right.left);
}
```

##### 迭代

```java
/**
 * 101. 对称二叉树（版本 2：迭代）
 *
 * @param root 根节点
 * @return 二叉树是否镜像对称
 */
public boolean isSymmetricV2(TreeNode root) {
    if (root == null) {return true;}

//  使用一个队列模拟同时存在两棵相同的二叉树，然后判断这两棵二叉树是否镜像对称
    Queue<TreeNode> queue = new LinkedList<>();

queue.offer(root);
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode left = queue.poll();
        TreeNode right = queue.poll();

if (left == null && right == null) {continue;}
        if (left == null || right == null) {return false;}
        if (left.val != right.val) {return false;}

queue.offer(left.left);
        queue.offer(right.right);

queue.offer(left.right);
        queue.offer(right.left);
    }

return true;
}
```

### 验证二叉搜索树

> 题目内容详见[98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree)。

#### 问题分析

1. 对于二叉树的题目，我们一般可以考虑一下看是否能**利用二叉树的三种深度优先遍历和一种广度优先遍历方法来解决**。
2. 在该题目中，我们可以利用**中序遍历**，只要判断**每一个遍历的节点的值是否都大于前一个节点**，进而就可以判断该二叉树是否为二叉搜索树。

#### 参考代码

##### 递归

```java
long pre = Long.MIN_VALUE;

/**
 * 98. 验证二叉搜索树（版本 1：递归（中序遍历））
 * @param root  根节点
 * @return  是否为有效的二叉搜索树
 */
public boolean isValidBSTV1(TreeNode root) {
    if (root == null) {return true;}

if (!isValidBSTV1(root.left)) {return false;} /*访问左子树：判断左子树是否为二叉搜索树*/
    if (root.val <= pre) {return false;}    /*访问根节点：判断根节点的值是否大于等于中序遍历的前一个节点的值*/
    pre = root.val; /*将当前节点保存为前一个节点*/
    return isValidBSTV1(root.right);  /*访问右子树：判断右子树是否为二叉搜索树*/
}
```

##### 迭代

```java
long pre = Long.MIN_VALUE;

/**
 * 98. 验证二叉搜索树（版本 2：迭代（中序遍历））
 * @param root  根节点
 * @return  是否为有效的二叉搜索树
 */
public boolean isValidBSTV2(TreeNode root) {
    if (root == null) {return true;}

Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;

while (!stack.empty() || cur != null) {
        while(cur != null) {    /*尽可能将这个节点的左子树入栈，相当于访问左子树*/
            stack.push(cur);
            cur = cur.left;
        }
        TreeNode node = stack.pop();    /*相当于访问根节点，然后判断根节点的值是否大于等于中序遍历的前一个节点的值*/
        if (node.val <= pre) {return false;}
        pre = node.val;
        if (node.right != null) {cur = node.right;} /*相当于访问右子树*/
    }

return true;
}
```

### 二叉树的完全性检验

> 题目内容详见[958. 二叉树的完全性检验](https://leetcode-cn.com/problems/check-completeness-of-a-binary-tree)。

#### 问题分析

1. 对于二叉树的题目，我们一般可以考虑一下看是否能**利用二叉树的三种深度优先遍历和一种广度优先遍历方法来解决**。
2. 该题目可以通过[层序遍历]()来解决，判断的依据就是，**如果一层中出现了一个为空的节点**，**并且后面还有节点，那么该二叉树就不是一个完全二叉树**，**如果后面没有节点**，**那么该二叉树就是一个完全二叉树**，因此，相比于层序遍历来说，该方法在**将当前节点的左节点和右节点添加到队列时不需要判断当前节点的左节点和右节点是否为空**。

#### 参考代码

```java
//  判断是否到达了二叉树末尾，只要层序遍历时遇到一个空节点，就认为到达了二叉树末尾
boolean reachEnd = false;

/**
 * 958. 二叉树的完全性检验（层序遍历）
 * @param root  根节点
 * @return  当前二叉树是否为完全二叉树
 */
public boolean isCompleteTree(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();

queue.add(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        //  如果到达了二叉树末尾，但后面还有非空节点，则该二叉树不是完全二叉树
        if (reachEnd && node != null) {
            return false;
        }
        //  只要层序遍历时遇到一个空节点，就认为到达了二叉树末尾，令 reachEnd 为 true，然后进行下一个节点的遍历
        if (node == null) {
            reachEnd = true;
            continue;
        }
        queue.add(node.left);
        queue.add(node.right);
    }

return true;
}
```

### 二叉搜索树的第 k 大节点

> 题目内容详见[剑指 Offer 54. 二叉搜索树的第 k 大节点](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof)。

#### 问题分析

1. 该题目解法基于**二叉树中序遍历为递增序列**这一性质，可以得到**二叉树中序遍历倒序为递减序列**。
2. 因此，**求二叉树第 $k$ 大的节点可以转化为求二叉树的中序遍历倒序的第 $k$ 个节点**。

#### 参考代码

```java
/**
 * 剑指 Offer 54. 二叉搜索树的第 k 大节点（中序遍历倒序）
 * @param root  根节点
 * @param k 最值序号
 * @return  二叉搜索树的第 k 大节点
 */
public int kthLargest(TreeNode root, int k) {
    //  base case
    if (root == null) {
        return -1;
    }
    TreeNode cur = root;
    //  用来模仿递归解法中的栈
    Stack<TreeNode> stack = new Stack<>();
    while (!stack.empty() || cur != null) {
        //  尽可能将这个节点的右子树入栈，相当于访问右子树
        while (cur != null) {
            stack.push(cur);
            cur = cur.right;
        }
        //  相当于访问根节点
        TreeNode node = stack.pop();
        if (--k == 0) {return node.val;}
        //  相当于访问左节点
        if (node.left != null) {
            cur = node.left;
        }
    }

return -1;
}
```

### 括号生成

> 题目内容详见[22. 括号生成](https://leetcode-cn.com/problems/generate-parentheses)。

#### 问题分析

1. 这一类问题是**在一棵隐式的树上求解**，**一般用**[深度优先遍历](https://notebook.ricear.com/project-21/doc-724/#1-1-%E6%B7%B1%E5%BA%A6%E4%BC%98%E5%85%88%E9%81%8D%E5%8E%86%E7%AE%97%E6%B3%95)**来解决**。
2. 我们以 $n = 2$ 为例，画树形结构图，方法是**做减法**。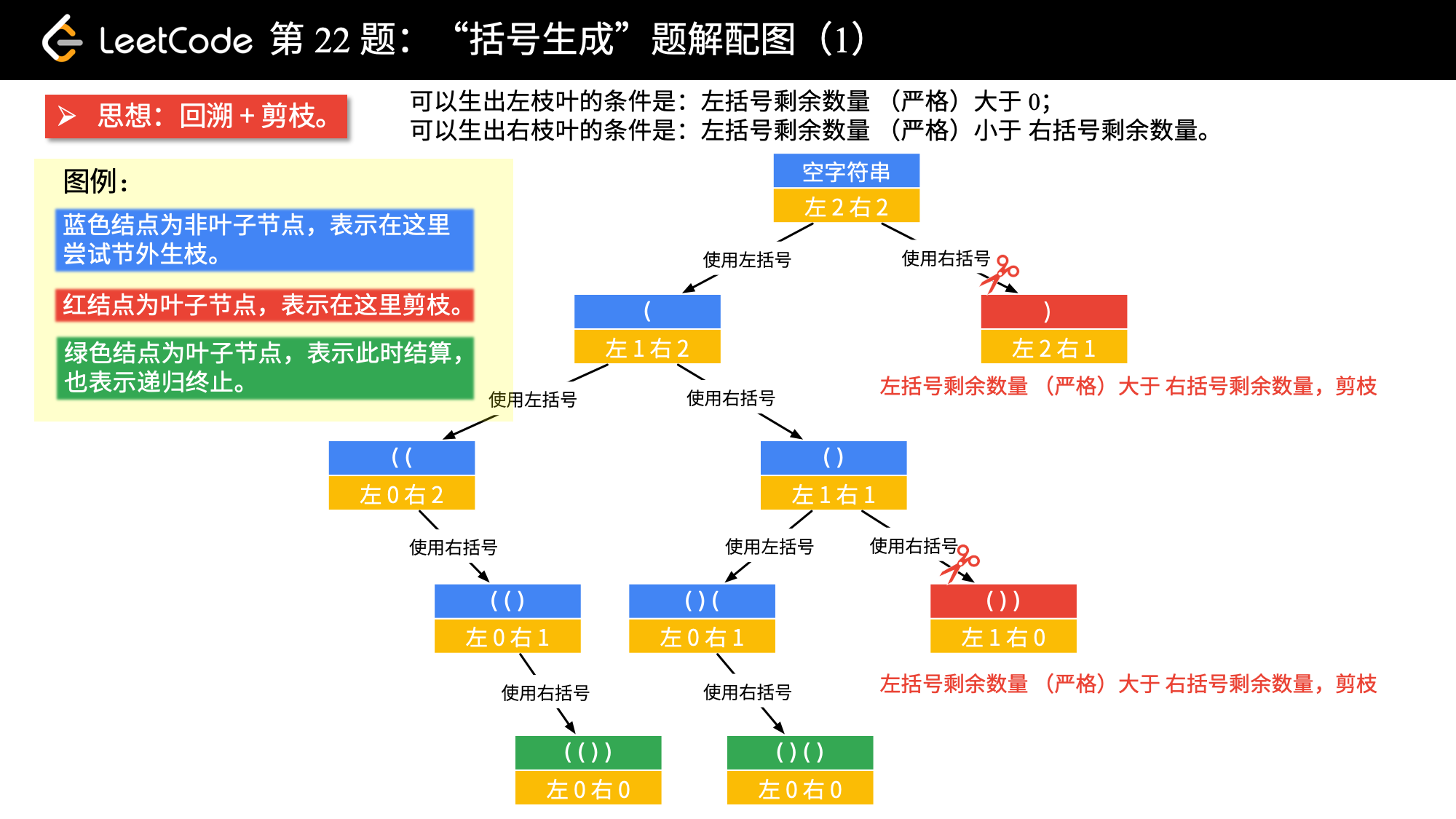![](https://notebook.ricear.com/media/202111/2021-11-13_2156250.32776863153577696.png)
   通过上图，我们可以得出如下结论：
   1. **当前左右括号的剩余个数都大于 0 时**，**才会产生分支**。
   2. **产生左分支的时候**，**只看当前是否还有左括号可以使用**。
   3. **产生右分支的时候**，**还受到左分支的限制**，**只有右括号的剩余个数严格大于左括号时**，**才可以产生分支**。
   4. **在左括号和右括号的剩余个数都等于 0 的时候结算**。

#### 参考代码

```java
/**
 * 22. 括号生成
 *
 * @param n 生成括号的对数
 * @return 能够生成所有可能的并且 有效的 括号组合
 */
public List<String> generateParenthesis(int n) {
    List<String> res = new ArrayList<>();
    if (n == 0) {return res;}
    dfs("", n, n, res);
    return res;
}

/**
 * 采用深度优先遍历求能够生成指定括号对数的所有可能且有效的括号组合
 *
 * @param curStr 当前字符串
 * @param left   左括号剩余个数
 * @param right  右括号剩余个数
 * @param res    生成的括号组合
 */
public void dfs(String curStr, int left, int right, List<String> res) {
    //  当左边和右边剩余的括号数都等于 0 的时候结算
    if (left == 0 && right == 0) {
        res.add(curStr);
        return;
    }

//  如果左括号剩余个数严格大于右括号剩余个数，则进行剪枝
    if (left > right) {
        return;
    }

//  向左遍历
    if (left > 0) {dfs(curStr + "(", left - 1, right, res);}
    //  向右遍历
    if (right > 0) {dfs(curStr + ")", left, right - 1, res);}
}
```

### 二叉搜索树与双向链表

> 题目内容详见[剑指 Offer 36. 二叉搜索树与双向链表](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof)。

#### 问题分析

1. 本题主要包含三个要素：
   1. **排序链表**：**节点应从小到大排列**，由于**二叉搜索树的中序遍历为递增序列**，因此**可以使用中序遍历来访问树的节点**。
   2. **双向链表**：**在构建相邻接点的引用关系时**，**设前驱结点为 $pre$ 和当前节点 $cur$**，**不仅应构建 $pre.right = cur$**，**也应构建 $cur.left = pre$**。
   3. **循环链表**：**设链表头结点为 $head$ 和尾节点 $tail$**，**则应构建 $head.left = tail$ 和 $tail.right =  head$**。

#### 参考代码

```java
/**
 * 剑指 Offer 36. 二叉搜索树与双向链表
 * @param root  二叉树根节点
 * @return  二叉搜索树转化后得到的排序的循环双向链表
 */
public Node treeToDoublyList(Node root) {
    if (root == null) {return null;}
    dfs(root);
    head.left = pre;
    pre.right = head;
    return head;
}

/**
 * 二叉树中序遍历
 * @param cur   当前节点
 */
public void dfs(Node cur) {
    if (cur == null) {return;}
    dfs(cur.left);
    if (pre != null) {pre.right = cur;}
    else {head = cur;}
    cur.left = pre;
    pre = cur;
    dfs(cur.right);
}
```

### 二叉树最大宽度

> 题目内容详见[662. 二叉树最大宽度](https://leetcode.cn/problems/maximum-width-of-binary-tree)。

#### 问题分析

1. **对于一棵完全二叉树**，**如果按照从上至下**，**从左往右对所有节点从零开始顺序编号**，**假设父节点的序号为 $i$**，**则**：

1. **左孩子节点的序号为 $ 2 * i + 1$**，**右孩子节点的序号为 $ 2 * i + 2$**。

2. **假设每层的宽度为 $width$**，**每层最后一个节点的序号为 $r$**，**每层第一个节点的序号为 $l$**，则

$$
      width = r - l + 1
      $$

#### 参考代码

```java
/*
 * 自定义树节点
 */
public class CustomTreeNode {
    TreeNode node;
    int position;
    public CustomTreeNode(TreeNode _node, int _position) {
        node = _node;
        position = _position;
    }
}

/*
 * 662. 二叉树最大宽度
 * @param root  二叉树根节点
 * @return  二叉树的最大宽度
 */
public int widthOfBinaryTree(TreeNode root) {
    if (root == null) {return 0;}
    int res = Integer.MIN_VALUE;
    Queue<CustomTreeNode> queue = new LinkedList<>();
    queue.offer(new CustomTreeNode(root, 1));
    while (!queue.isEmpty()) {
        int n = queue.size();
        CustomTreeNode left = new CustomTreeNode(null, 0); //  每一层最左边节点
        CustomTreeNode right = new CustomTreeNode(null, 0); //  每一层最右边节点
        for (int i = 0; i < n; i++) {
            CustomTreeNode node = queue.poll();
            if (i == 0) {left = node;}
            if (i == n - 1) {right = node;}
            if (node.node.left != null) {queue.offer(new CustomTreeNode(node.node.left, 2 * node.position));}
            if (node.node.right != null) {queue.offer(new CustomTreeNode(node.node.right, 2 * node.position + 1));}
        }
        res = Math.max(res, right.position - left.position + 1);
    }
    return res;
}
```

### 二叉树的序列化与反序列化

> 题目内容详见[297. 二叉树的序列化与反序列化](https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree)。

#### 问题分析

1. 这道题目可以采用[深度优先遍历](https://notebook.ricear.com/project-21/doc-724/#1-1-%E6%B7%B1%E5%BA%A6%E4%BC%98%E5%85%88%E9%81%8D%E5%8E%86%E7%AE%97%E6%B3%95)的方法来求解：
   1. **序列化**：
      1. **递归遍历一棵树**，**重点关注当前节点**，**他的子树的遍历交给递归来完成**，即 `serialize`**函数**，**你帮我分别序列化我的左右子树**，**我等你返回的结果**，**再拼接一下**。
      2. **选择前序遍历**，**是因为 $ 根 \rightarrow 左 \rightarrow 右 $ 的打印顺序**，**在反序列化时更容易定位出根节点的值**。
      3. **遇到 `null` 节点也要翻译成特定符号**，**反序列化时才知道这里是 `null`**。![image.png](https://notebook.ricear.com/media/202201/2022-01-09_1736130.3886432153851599.png)
   2. **反序列化**：
      1. **反序列化一样**，**也是递归**。
      2. **前序遍历的序列化字符串**，**如下图所示**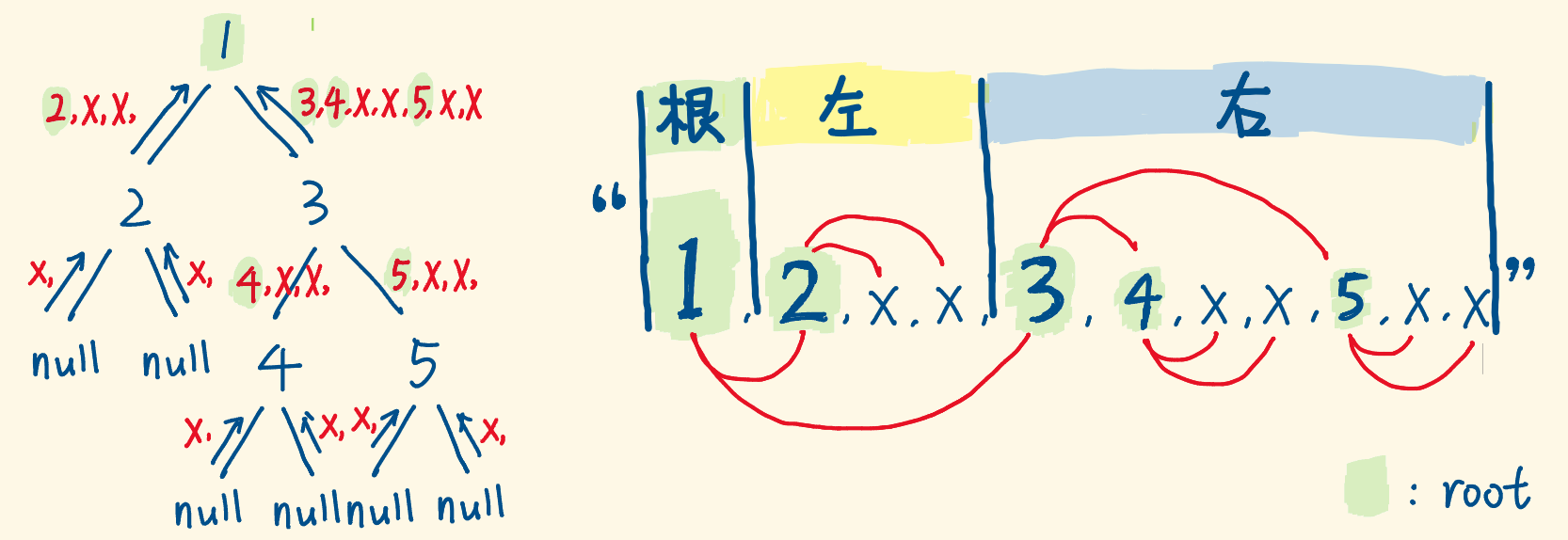：![image.png](https://notebook.ricear.com/media/202201/2022-01-09_1738130.8641382032786079.png)
      3. **我们可以定义函数 `buildTree()` 用于还原二叉树**，**传入由序列化字符串转成的数组 $arr$**。
      4. **然后逐个遍历 $arr$ 中的元素**，**构建当前子树的根节点**，**顺着 $arr$**，**构建顺序是根节点**、**左子树**、**右子树**：
         1. **如果当前遍历的字符为 `X`**，**则返回 `null` 节点**。
         2. **如果弹出的字符是数字**，**则创建 `root` 节点**，**并递归构建 `root` 的左右子树**，**最后返回 `root`**。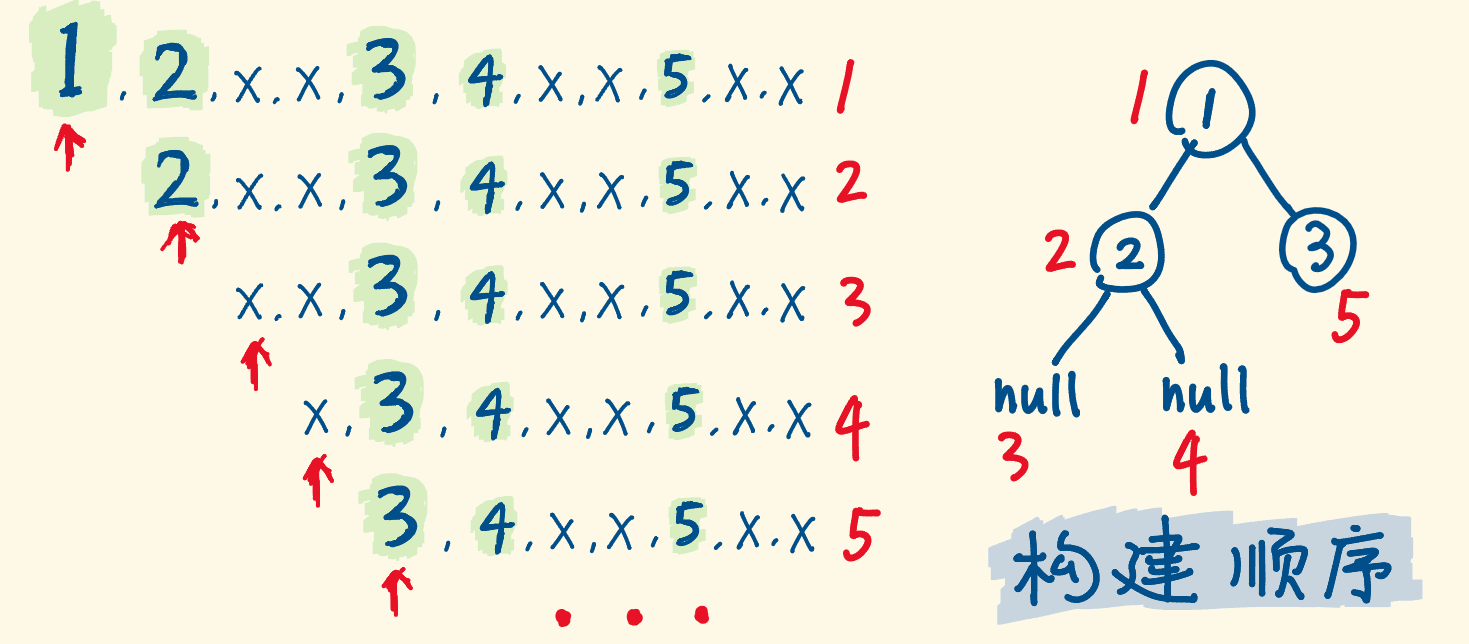![image.png](https://notebook.ricear.com/media/202201/2022-01-09_1743510.06430358234861278.png)

#### 参考代码

```java
/**
 * 使用层序遍历对二叉树进行序列化
 * @param root  二叉树头结点
 * @return  二叉树序列化后的字符串
 */
public String serialize(TreeNode root) {
    if (root == null) {return "";}
    StringBuffer sb = new StringBuffer();
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        if (node != null) {
            queue.offer(node.left);
            queue.offer(node.right);
            sb.append(node.val);
        } else {
            sb.append("X"); //  将空节点序列化为 X
        }
        sb.append(","); //  将不同节点之间添加分隔符
    }
    return sb.toString().substring(0, sb.length() - 1);
}
/**
 * 使用层序遍历对二叉树进行反序列化
 * @param data  二叉树序列化后的字符串
 * @return  反序列化后的二叉树的头结点
 */
public TreeNode deserialize(String data) {
    if (data.equals("")) {return null;}
    String[] split = data.split(",");
    int index = 0;  //  当前节点的位置
    TreeNode root = new TreeNode(Integer.parseInt(split[index]));
    Queue<TreeNode> queue = new LinkedList();
    queue.offer(root);
    while (index < split.length - 2) {
        TreeNode node = queue.poll();
        String leftVal = split[index + 1];  //  左节点
        String rightVal = split[index + 2]; //  右节点
        if (!leftVal.equals("X")) { //  左节点不为空，则反序列化左节点
            TreeNode leftNode = new TreeNode(Integer.parseInt(leftVal));
            node.left = leftNode;
            queue.offer(node.left);
        }
        if (!rightVal.equals("X")) {    //  右节点不为空，则反序列化又节点 
            TreeNode rightNode = new TreeNode(Integer.parseInt(rightVal));
            node.right = rightNode;
            queue.offer(node.right);
        }
        index += 2; //  每次反序列化两个节点
    }
    return root;
}
```

### 树的子结构

> 题目内容详见[剑指 Offer 26. 树的子结构](https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof)。

#### 问题分析

1. 这道题目可以采用[深度优先遍历](https://notebook.ricear.com/project-21/doc-724/#1-1-%E6%B7%B1%E5%BA%A6%E4%BC%98%E5%85%88%E9%81%8D%E5%8E%86%E7%AE%97%E6%B3%95)的方法来求解：
   1. 如果**两棵树的顶点相同**，则**分别判断两棵树对应的左子树和右子树是否相同**。
   2. 如果**两棵树的顶点不相同**，则**分别判断 $B$ 是否为 $A$ 的左子树或右子树的子结构**。

#### 参考代码

```java
/**
 * 剑指 Offer 26. 树的子结构
 * @param A 第一个二叉树
 * @param B 第二个二叉树
 * @return  B 是否为 A 的子结构
 */
public boolean isSubStructure(TreeNode A, TreeNode B) {
    return (A != null && B != null) && (dfs(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B));
}

/**
 * 判断在顶点相同的情况下 B 是否为 A 的子结构
 * @param A 第一个二叉树
 * @param B 第二个二叉树
 * @return  在顶点相同的情况下 B 是否为 A 的子结构
 */
public boolean dfs(TreeNode A, TreeNode B) {
    if (B == null) {return true;}
    if (A == null || A.val != B.val) {return false;}
    return dfs(A.left, B.left) && dfs(A.right, B.right);
}
```

### 平衡二叉树

> 题目内容详见[110. 平衡二叉树](https://leetcode-cn.com/problems/balanced-binary-tree)。

#### 问题分析

> 注：下面所说的高度指**距离子树底部的高度**。

1. 自底向上判断二叉树是否为平衡二叉树的基本思路为：
   1. 按照类似于**后序遍历**的方法判断**当前节点是否为平衡二叉树**，判断标准为：
      1. 当前节点的**左右子树均为平衡二叉树**。
      2. 当前节点的**左右子树高度差小于 2**。
   2. 如果当前节点**不是平衡二叉树**，则直接**返回-1**。
   3. 如果当前节点**是平衡二叉树**，则**当前节点的高度为左右子树高度的最大值加1**。
2. 算法的演示动画可参考[平衡二叉树](https://leetcode-cn.com/problems/balanced-binary-tree/solution/ping-heng-er-cha-shu-by-leetcode-solution)。
3. 该算法**不存在自顶向下算法中的重复遍历问题**。

#### 参考代码

```java
/**
 * 110. 平衡二叉树（后序遍历）
 * @param root  根节点
 * @return  二叉树是否为平衡二叉树
 */
public boolean isBalanced(TreeNode root) {
    if (root == null) {return true;}
    return heightV2(root) != -1;
}

/**
 * 计算一个二叉树的高度
 * @param root  根节点
 * @return  二叉树的高度
 */
public int height(TreeNode root) {
    //  base case
    if (root == null) {return 0;}
    //  左子树高度
    int leftHeight = height(root.left);
    //  右子树高度
    int rightHeight = height(root.right);
    //  如果左子树不是平衡二叉树或者右子树不是平衡二叉树或者左右子树的高度差大于等于 2，则当前子树不是平衡二叉树
    if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) >= 2) {
        return -1;
    }
    //  如果当前子树是平衡二叉树，则返回当前子树的高度
    return Math.max(leftHeight, rightHeight) + 1;
}
```

### 二叉树的最近公共祖先

> 题目内容详见[236. 二叉树的最近公共祖先](https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree)。

#### 问题分析

1. 首先创建相关变量：
   1. $stack$：存储根节点到遍历节点的遍历路径。
   2. $res$、$res2$：分别存储 $p$、$q$ 的遍历节点信息。
2. 然后对二叉树进行前序遍历：
   1. 将 $root$ 入栈。
   2. 如果 $root=p$：
      1. 将栈中的信息存入 $res$。
      2. 将 $res$ 中的信息存入 $stack$，用于后面的遍历。
   3. 如果 $root=q$：
      1. 将栈中的信息存入 $res2$。
      2. 将 $res2$ 中的信息存入 $stack$，用于后面的遍历。
   4. 递归遍历左子树。
   5. 递归遍历右子树。
   6. 如果栈的大小大于 0，则将栈中的元素弹出。
3. 获取 $res$ 和 $res2$ 长度的最小值 $size$。
4. 然后对 $size$ 从 $i=0$ 开始遍历：
   1. 如果 $res$ 的长度大于 $res2$：
      1. 如果 $res2$ 中第 $i$ 个元素等于 $res$ 中第 $res.size()-size+i$ 个元素，则返回 $res2$ 的第 $i$ 个元素。
   2. 如果 $res2$ 的长度大于 $res$：
      1. 如果 $res$ 中第 $i$ 个元素等于 $res2$ 中第 $res2.size()-size+i$ 个元素，则返回 $res$ 的第 $i$ 个元素。
5. 如果上面的条件都不成立，则最后返回 $null$。

![](https://notebook.ricear.com/media/202106/236-二叉树的最近公共祖先（解法一：前序遍历）_1624369019.gif)

#### 参考代码

```java
Stack<TreeNode> stack = new Stack<>();

/**
 * 236. 二叉树的最近公共祖先
 * @param root  二叉树根节点
 * @param o1    待查询的第一个节点的值
 * @param o2    待查询的第二个节点的值
 * @return  两个待查询的节点的最近公共祖先的值
 */
public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
    ArrayList<TreeNode> list1 = new ArrayList<>();
    ArrayList<TreeNode> list2 = new ArrayList<>();
    dfs(root, o1, o2, list1, list2);
    /**
     * 将两个 List 的元素的顺序调整为第一个元素为头结点的值，便于后面的比较
     */
    if (list1.get(0) != root) {
        for (int i = 0; i < list1.size() / 2; i++) {
        TreeNode temp = list1.get(i);
        list1.set(i, list1.get(list1.size() - 1 - i));
        list1.set(list1.size() - 1 - i, temp);
    }
    } if (list2.get(0) != root) {
        for (int i = 0; i < list2.size() / 2; i++) {
        TreeNode temp = list2.get(i);
        list2.set(i, list2.get(list2.size() - 1 - i));
        list2.set(list2.size() - 1 - i, temp);
    }
    }
    /**
     * 将两个 List 对齐后返回第一个相等的元素，即为两个节点的最近公共祖先
     */
    int minSize = Math.min(list1.size(), list2.size());
    for (int i = minSize - 1; i >= 0; i--) {
        if (list1.get(i).val == list2.get(i).val) {return list1.get(i).val;}
    }
    return 0;
}

/**
 * 递归获取二叉树两个指定节点的路径（前序遍历）
 * @param root  二叉树头结点
 * @param num1  待查询的第一个节点的值
 * @param num2  待查询的第二个节点的值
 * @param list1 存储二叉树中头结点到 num1 的路径
 * @param list2 存储二叉树中头结点到 num2 的路径
 */
public void dfs (TreeNode root, int num1, int num2, ArrayList<TreeNode> list1, ArrayList<TreeNode> list2) {
    if (root == null) {return;}
    stack.push(root);
    /**
     * 如果当前节点的值等于 num1 或 num2，则更新相应节点的路径，同时恢复栈原来的状态
     */
    if (root.val == num1) {
        while (!stack.empty()) {
            list1.add(stack.pop());
        }
        for (int i = list1.size() - 1; i >= 0; i--) {
            stack.push(list1.get(i));
        }
    } else if (root.val == num2) {
        while (!stack.empty()) {
            list2.add(stack.pop());
        }
        for (int i = list2.size() - 1; i >= 0; i--) {
            stack.push(list2.get(i));
        }
    }
    dfs(root.left, num1, num2, list1, list2);   //  遍历左子树
    dfs(root.right, num1, num2, list1, list2);  //  遍历右子树
    if (stack.size() > 0) {stack.pop();}    //  如果栈中元素的个数大于 0，则弹出栈中的元素
}
```

> 该题目同样可以采用 [回溯法](https://notebook.ricear.com/project-21/doc-737) 来求解，核心思路为先通过回溯法得到 **根节点到两个节点的路径**，然后根据两个节点的路径找到他们的最近公共祖先。
>
> ~~~java
> List<TreeNode> list1 = null;  // 存储根节点到节点 p 的路径
> List<TreeNode> list2 = null;  // 存储根节点到节点 q 的路径
> LinkedList<TreeNode> list = new LinkedList<>();  // 临时存储当前遍历得到的节点的路径
> boolean[] pathDone = new boolean[2];  // 判断两个节点的路径是否获取完成
> 
> /**
>  * 二叉树的最近公共祖先
>  * 
>  * @param root 根节点
>  * @param p 其中一个节点
>  * @param q 另一个节点
>  */
> public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
>     TreeNode r = root;
>     backtrack(r, p, q);  // 回溯法获取根节点到 p 和 q 的路径
>     for (int i = Math.min(list1.size(), list2.size()) - 1; i >= 0; i--) {
>         if (list1.get(i).val == list2.get(i).val) {return list1.get(i);}  // 根据路径获取两个节点的最近公共祖先
>     }
>     return null;
> }
> 
> /**
>  * 回溯法获取根节点到两个节点的路径
>  * 
>  * @param root 根节点
>  * @param p 其中一个节点
>  * @param q 另一个节点
>  */
> public void backtrack(TreeNode root, TreeNode p, TreeNode q) {
>     if (pathDone[0] && pathDone[1]) {return;}  // p 和 q 的路径都已经获取完成
>     if (root == null) {return;}
>     
>     list.addLast(root);  // 做选择
>     if (root.val == p.val) {list1 = new ArrayList<>(list);pathDone[0] = true;}  // p 节点遍历完成
>     if (root.val == q.val) {list2 = new ArrayList<>(list);pathDone[1] = true;}  // q 节点遍历完成
>     backtrack(root.left, p, q);  // 遍历左子树
>     backtrack(root.right, p, q);  // 遍历右子树
>     list.removeLast();  // 撤销选择
> }
> ~~~

## 参考文献

1. [图解 二叉树的四种遍历](https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/tu-jie-er-cha-shu-de-si-chong-bian-li-by-z1m)。
2. [BFS 的使用场景总结：层序遍历、最短路径问题](https://leetcode-cn.com/problems/binary-tree-level-order-traversal/solution/bfs-de-shi-yong-chang-jing-zong-jie-ceng-xu-bian-l)。
3. [103. 二叉树的锯齿形层序遍历](https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal)。
4. [226. 翻转二叉树](https://leetcode-cn.com/problems/invert-binary-tree)。
5. [动画演示 两种实现 226. 翻转二叉树](https://leetcode-cn.com/problems/invert-binary-tree/solution/dong-hua-yan-shi-liang-chong-shi-xian-226-fan-zhua)。
6. [101. 对称二叉树](https://leetcode-cn.com/problems/symmetric-tree)。
7. [对称二叉树](https://leetcode-cn.com/problems/symmetric-tree/solution/dui-cheng-er-cha-shu-by-leetcode-solution)。
8. [958. 二叉树的完全性检验](https://leetcode-cn.com/problems/check-completeness-of-a-binary-tree)。
9. [层序遍历](https://leetcode-cn.com/problems/check-completeness-of-a-binary-tree/solution/ceng-xu-bian-li-by-dian-dao-de-hu-die-681d)。
10. [剑指 Offer 54. 二叉搜索树的第 k 大节点](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof)。
11. [面试题 54. 二叉搜索树的第 k 大节点（中序遍历 + 提前返回，清晰图解）](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/solution/mian-shi-ti-54-er-cha-sou-suo-shu-de-di-k-da-jie-d)。
12. [22. 括号生成](https://leetcode-cn.com/problems/generate-parentheses)。
13. [回溯算法（深度优先遍历）+ 广度优先遍历（Java）](https://leetcode-cn.com/problems/generate-parentheses/solution/hui-su-suan-fa-by-liweiwei1419)。
14. [剑指 Offer 36. 二叉搜索树与双向链表](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof)。
15. [剑指 Offer 36. 二叉搜索树与双向链表（中序遍历，清晰图解）](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/solution/mian-shi-ti-36-er-cha-sou-suo-shu-yu-shuang-xian-5)。
16. [二叉树最大宽度](https://leetcode-cn.com/problems/maximum-width-of-binary-tree/solution/er-cha-shu-zui-da-kuan-du-by-leetcode)。
17. [BFS+ 完全二叉树性质（看完不会来揍我）](https://leetcode-cn.com/problems/maximum-width-of-binary-tree/solution/bfswan-quan-er-cha-shu-xing-zhi-kan-wan-qmguc)。
18. [297. 二叉树的序列化与反序列化](https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree)。
19. [『手画图解』剖析 DFS、BFS 解法 | 二叉树的序列化与反序列化](https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/solution/shou-hui-tu-jie-gei-chu-dfshe-bfsliang-chong-jie-f)。
20. [剑指 Offer 26. 树的子结构](https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof)。
21. [110. 平衡二叉树](https://leetcode-cn.com/problems/balanced-binary-tree)。
22. [平衡二叉树](https://leetcode-cn.com/problems/balanced-binary-tree/solution/ping-heng-er-cha-shu-by-leetcode-solution)。
23. [236. 二叉树的最近公共祖先](https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree)。
24. [236. 二叉树的最近公共祖先（后序遍历 DFS ，清晰图解）](https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/solution/236-er-cha-shu-de-zui-jin-gong-gong-zu-xian-hou-xu)。
25. [【C++ 经典递归】思路非常好理解 时间复杂度 O(n), 空间复杂度 O(n)](https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/solution/c-jing-dian-di-gui-si-lu-fei-chang-hao-li-jie-shi-)。