岛屿问题

## 前言

1. 我们所熟悉的 DFS（深度优先搜索）问题通常是在树或者图结构上进行的，而我们今天要讨论的 DFS 问题，是在一种【网格】结构中进行的，**岛屿问题是这类网格 DFS 问题的典型代表**。
2. 网格结构遍历起来要比二叉树复杂一些，如果没有掌握一定的方法，DFS 代码容易写得冗长繁杂。
3. 本文将以岛屿问题为例，展示网格类问题 DFS 通用思路，以及如何让代码变得简洁。

## 网格问题的基本概念

1. 我们首先要明确一下岛屿问题中的网格结构是如何定义的，以方便我们后面的讨论。
2. 网格问题是由 $m \times n$ 个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。
3. 岛屿问题是一类典型的网格问题，每个格子中的数字可能是 0 或者 1，我们把数字为 0 的格子看成海洋格子，数字为 1 的格子看成陆地格子，这样相邻的陆地格子就连接成一个岛屿。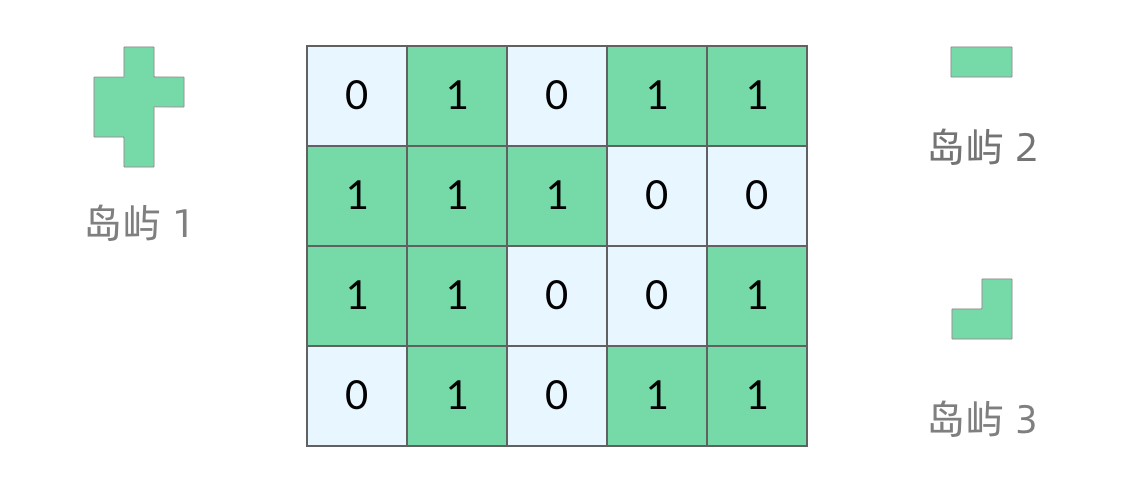

![岛屿问题示例](https://notebook.ricear.com/media/202107/2021-07-03_211007.png)

4. 在这样一个设定下，就出现了各种岛屿问题的变种，包括**岛屿的数量**、**面积**、**周长**等，不过这些问题，基本都可以用 DFS 遍历来解决。

## 网格 DFS 的基本结构

### 基本结构

1. 网格结构要比二叉树结构稍微复杂一些，他其实是一种**简化版的图结构**，要写好网格上的 DFS 遍历，我们首先要理解二叉树上的 DFS 遍历方法，再类比写出网格结构上的 DFS 遍历，我们写的[二叉树 DFS 遍历](https://notebook.ricear.com/project-21/doc-724/#1-1-1-%E5%89%8D%E5%BA%8F%E9%81%8D%E5%8E%86)一般是这样的：

```java
   void traverse(TreeNode root) {
       // 判断 base case
       if (root == null) {
           return;
       }
       // 访问两个相邻结点：左子结点、右子结点
       traverse(root.left);
       traverse(root.right);
   }
   ```
2. 可以看到，二叉树的 DFS 遍历有两个要素，分别为**判断 base case**和**访问相邻接点**：

1. 第一个要素是**判断 base case：**
      1. 一般来说，二叉树遍历的 `base case` 是 `root == null`，这样一个条件判断其实有两个含义：
         1. 一方面，这表示 `root`**指向的子树为空**，**不需要再往下遍历了**。
         2. 另一方面，**在 `root == null` 的时候及时返回**，**可以让后面的 `root.left` 和 `root.right` 操作不会出现空指针异常**。
   2. 第二个要素是**访问相邻接点：**
      1. **二叉树的相邻接点**非常简单，**只有左子树和右子树两个**。
      2. 二叉树本身就是一个**递归定义**的结构：**一棵二叉树**，**他的左子树和右子树也是一棵二叉树**，那么我们的 DFS 遍历只需要**递归调用左子树和右子树即可**。
3. 对于网格上的 DFS，我们完全可以参考二叉树的 DFS，写出网格 DFS 的两个要素：

1. 首先，**网格 DFS 中的** `base case` 从二叉树的 `base case` 对应过来，应该**是网格中不需要继续遍历**、$grid[r][c]$**会出现数组下标越界异常的格子**，也就是那些**超出网格范围的格子**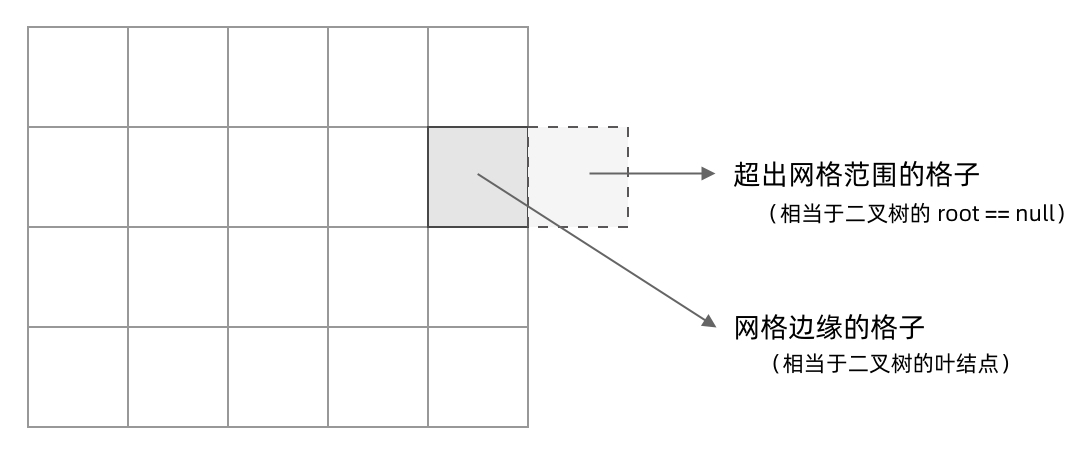：![网格 DFS 的 base case](https://notebook.ricear.com/media/202107/2021-07-03_213404.png)
   2. 其次，网格结构中的格子**有上下左右四个相邻的节点**，对于格子 $(r,c)$ 来说（$r$ 和 $c$ 分别代表行坐标和列坐标），四个相邻的格子分别是：

1. **上：$(r+1,c)$。**
      2. **下：**$(r-1,c)$。
      3. **左：$(r,c-1)$。**
      4. **右：$(r,c+1)$。**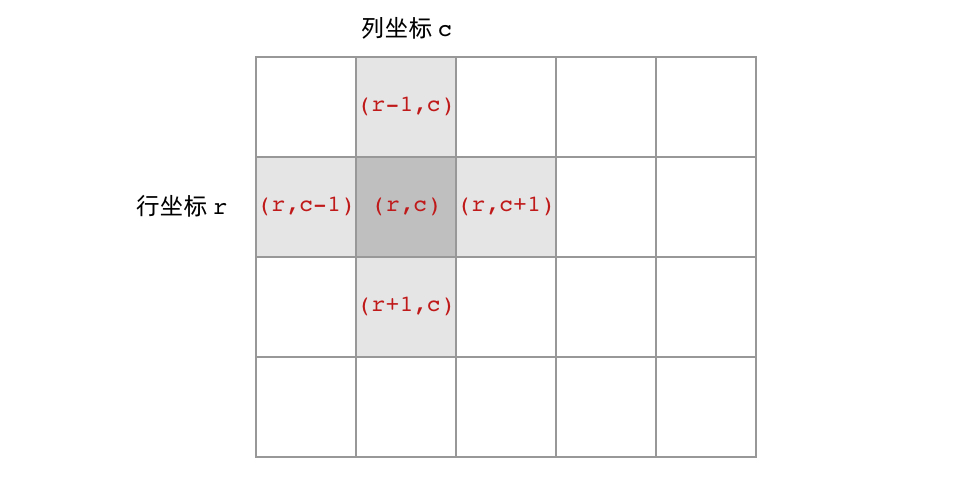

![网格结构中四个相邻的格子](https://notebook.ricear.com/media/202107/2021-07-03_213829.png)
4. 这样，我们得到了网格 DFS 遍历的框架代码：

```java
   /**
    * 判断是否在方格范围内
    * @param grid  方格数组
    * @param r 横坐标
    * @param c 纵坐标
    * @return  (r, c) 是否在方格范围内
    */
   public boolean inArea(int[][] grid, int r, int c) {
       return r >= 0 && r < grid.length
               && c >= 0 && c < grid[0].length;
   }
   
   /**
    * 方格 DFS 遍历算法（版本 1：未加重复遍历的判断）
    * @param grid  方格数组
    * @param r 横坐标
    * @param c 纵坐标
    */
   public void dfsV1(int[][] grid, int r, int c) {
       //  base case
       //  如果坐标 (r, c) 超出了网格范围，直接返回
       if (!inArea(grid, r, c)) {
           return;
       }
   
       //  访问上、下、左、右四个相邻接点
       dfsV1(grid, r + 1, c);
       dfsV1(grid, r - 1, c);
       dfsV1(grid, r, c - 1);
       dfsV1(grid, r, c + 1);
   }
   ```

### 完善后的结构（避免重复遍历）

1. 网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于**遍历中可能遇到遍历过的节点**，这是因为**网格结构本质上是一个图**，**我们可以把每个格子看成图中的节点**，**每个节点有上下左右的四条边**，**在图中遍历时**，**自然可能遇到重复遍历节点**，这时候，DFS 可能会不停地兜圈子，永远停不下来，如下图所示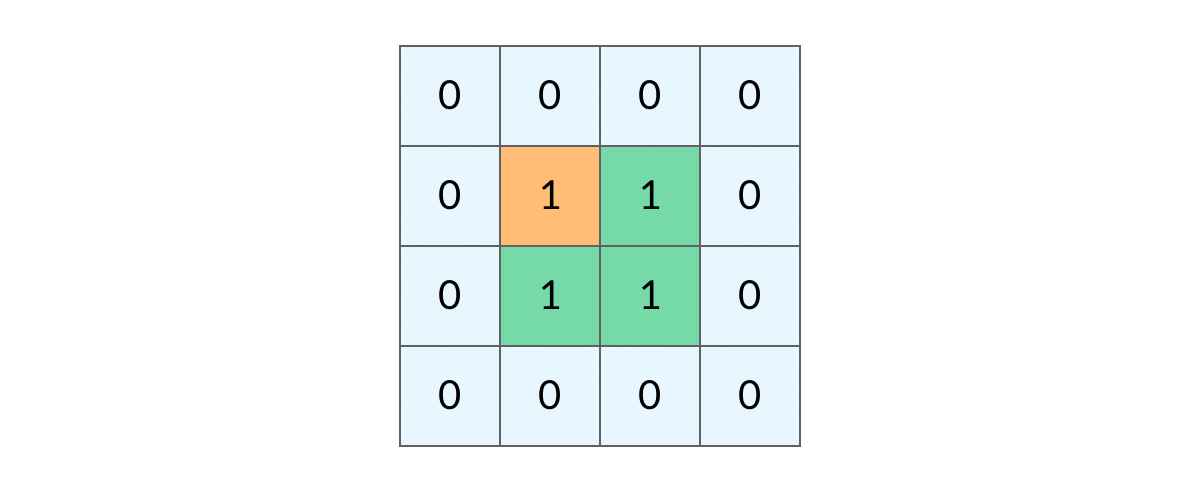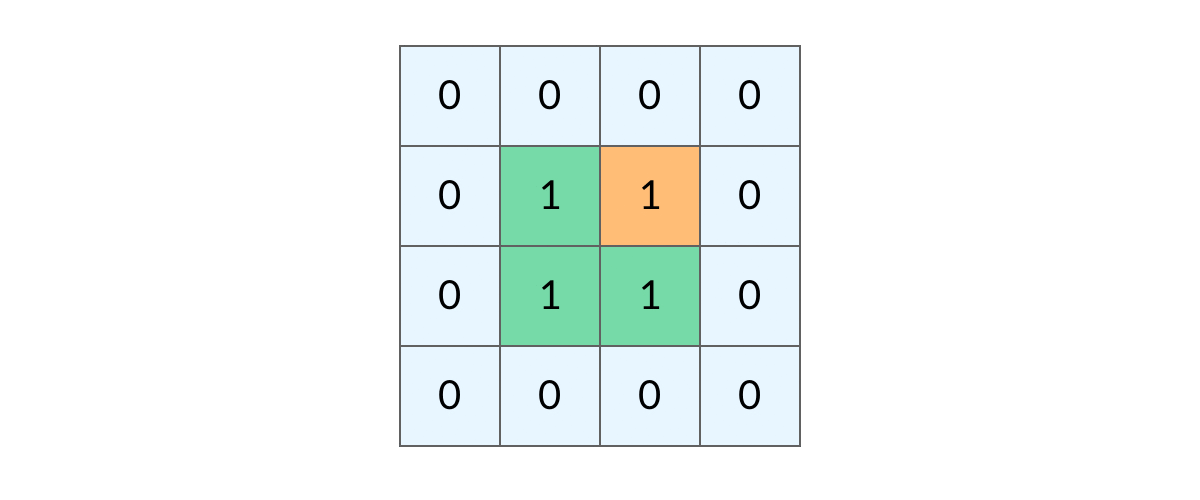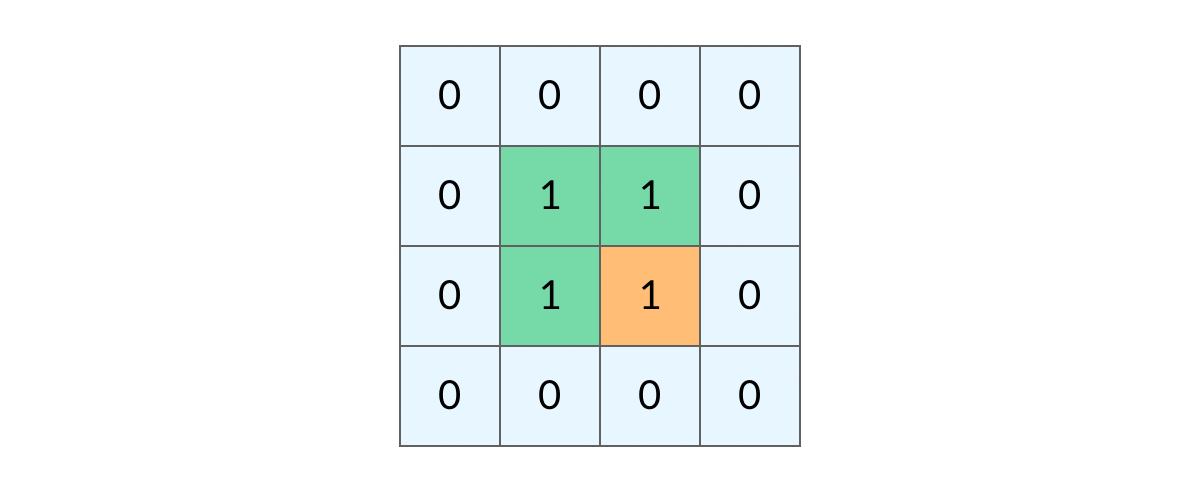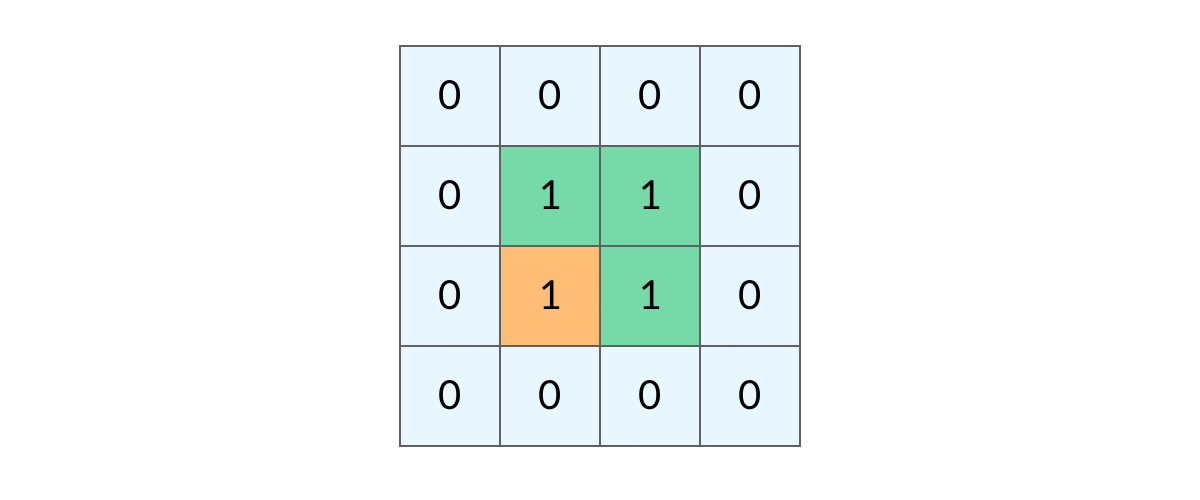：![DFS 遍历可能会兜圈子（动图）](https://notebook.ricear.com/media/202107/2021-07-04_190815.png)
2. 我们可以通过**标记已经遍历过的格子**来避免重复遍历问题，以岛屿问题为例：

1. 我们需要在所有值为 1 的陆地格子上做 DFS 遍历。
   2. 每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。
   3. 也就是说，每个格子可能取三个值：
      1. **0**：**海洋格子**。
      2. **1**：**陆地格子（未遍历过）**。
      3. **2**：**陆地格子（已遍历过）**。
3. 我们在框架中加入避免重复遍历的语句，具体如下：

```java
   /**
    * 判断是否在方格范围内
    * @param grid  方格数组
    * @param r 横坐标
    * @param c 纵坐标
    * @return  (r, c) 是否在方格范围内
    */
   public boolean inArea(int[][] grid, int r, int c) {
       return r >= 0 && r < grid.length
               && c >= 0 && c < grid[0].length;
   }
   
   /**
    * 方格 DFS 遍历算法（版本 2：加入重复遍历的判断）
    * @param grid  方格数组
    * @param r 横坐标
    * @param c 纵坐标
    */
   public void dfsV2(int[][] grid, int r, int c) {
       //  base case
       //  如果坐标 (r, c) 超出了网格范围，直接返回
       if (!inArea(grid, r, c)) {
           return;
       }
   
       //  如果这个格子不是 未遍历过的陆地，则直接返回
       if (grid[r][c] != 1) {
           return;
       }
       //  将当前陆地标记为 已遍历过
       grid[r][c] = 2;
   
       //  访问上、下、左、右四个相邻接点
       dfsV2(grid, r + 1, c);
       dfsV2(grid, r - 1, c);
       dfsV2(grid, r, c - 1);
       dfsV2(grid, r, c + 1);
   }
   ```
4. 加入重复遍历的判断之后的示意图如下所示：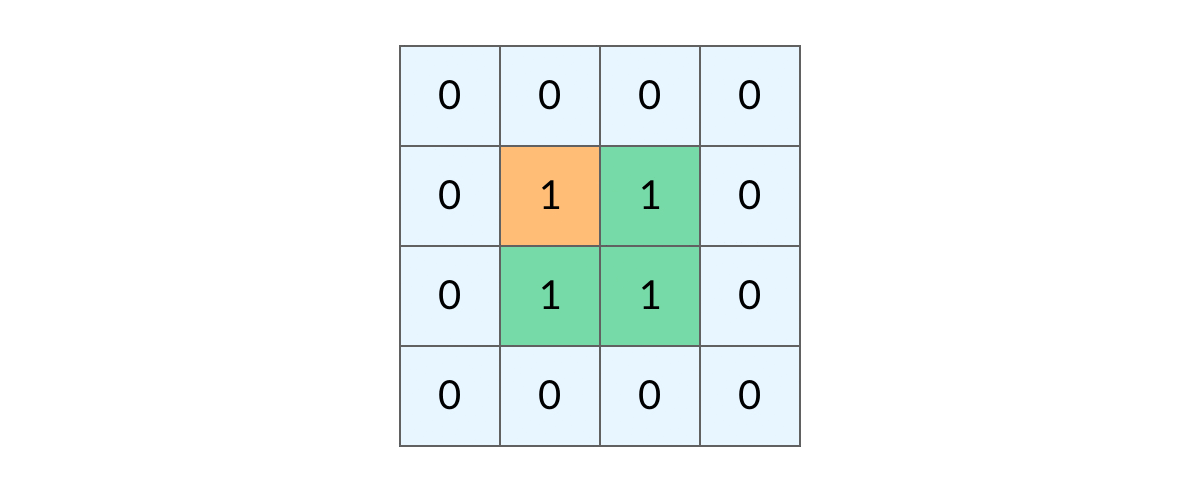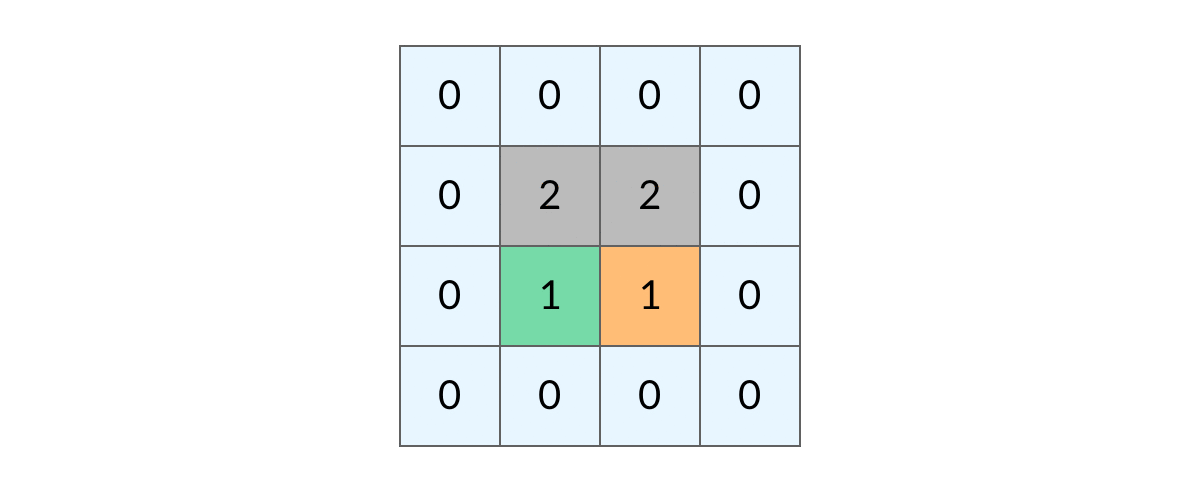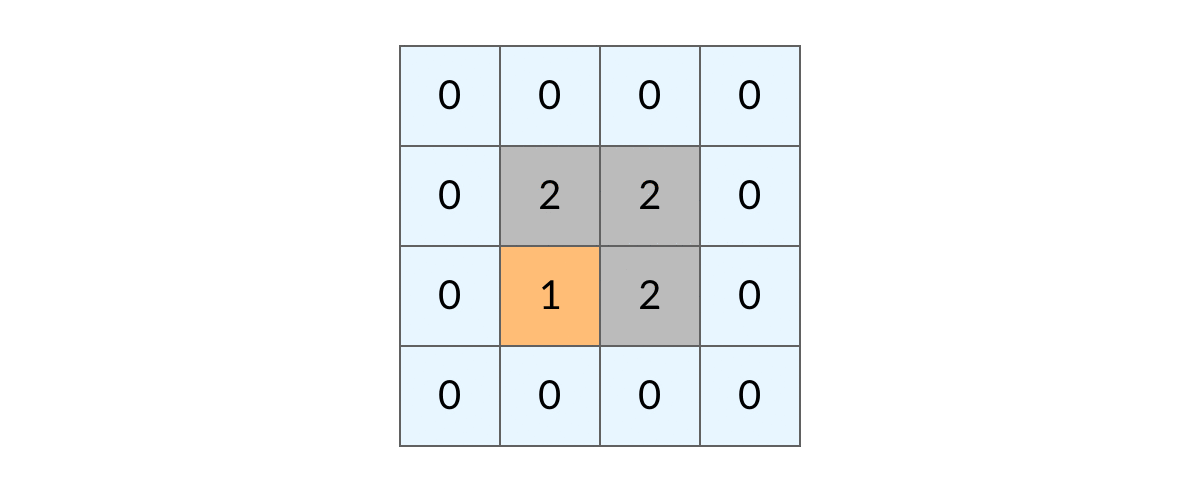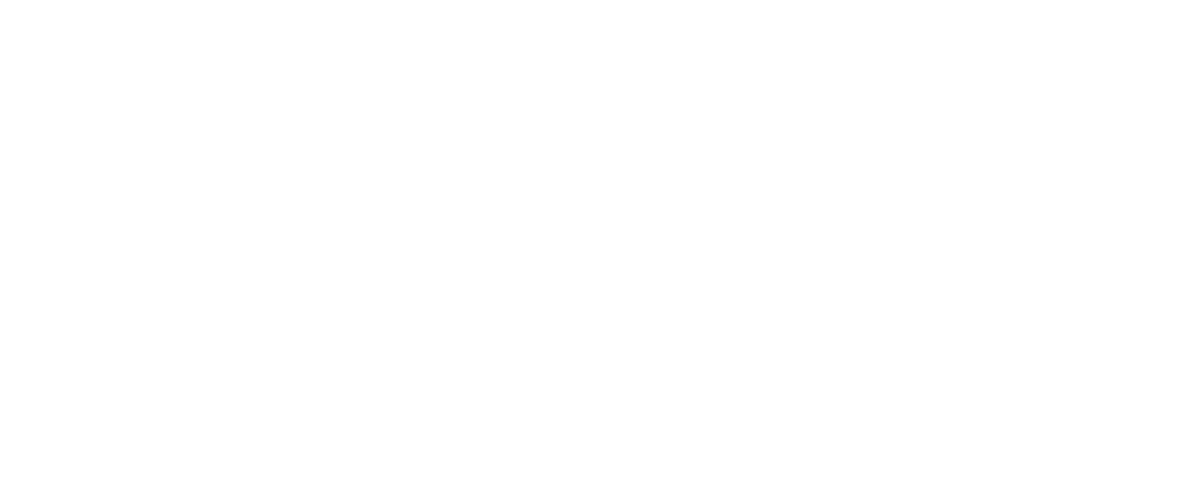

![标记已遍历的格子](https://notebook.ricear.com/media/202107/2021-07-04_192439.png)
5. 这样，我们就得到了一个岛屿问题、乃至各种网格问题的通用 DFS 遍历方法，以下所讲的几个例题，其实都只需要在 DFS 遍历框架上稍加修改而已。

## 相关题目

### 岛屿数量

#### 题目

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

**示例 1：**

```txt
输入：grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出：1
```

**示例 2：**

```txt
输入：grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出：3
```

**提示：**

* m == grid.length
* n == grid[i].length
* 1 <= m, n <= 300
* grid[i][j] 的值为 '0' 或 '1'

#### 问题分析

1. 这个直接根据模板进行修改一下即可，同时需要注意的是：
   1. **只要当遍历到的点是陆地的话才会开始执行 `dfs()` 函数**，因此**每当遍历一个陆地的点**，**岛屿数量看定会加 1**。
   2. **在 `dfs()` 函数中**，**会将已经遍历过的陆地标记为已遍历**，因此**下一次遍历到这块已遍历过的陆地时**，**会直接返回**。

#### 参考代码

```java
/**
 * 200. 岛屿数量
 * @param grid  网格
 * @return  网格中岛屿的数量
 */
public int numIslands(char[][] grid) {
    int res = 0;
    for (int i = 0; i < grid.length; i++) {
        for (int j = 0; j < grid[i].length; j++) {
            if (grid[i][j] == '1') {
                dfs(grid, i, j);
                res++;  /*将当前岛屿数量加 1*/
            }
        }
    }
    return res;
}

/**
 * 判断点 (r, c) 是否在网格范围内
 * @param grid  网格
 * @param r 横坐标
 * @param c 纵坐标
 * @return  (r, c) 是否在网格范围内
 */
public boolean inArea(char[][] grid, int r, int c) {
    return r >= 0 && r < grid.length && c >= 0 && c < grid[0].length;
}

/**
 * 网格深度优先遍历
 * @param grid  网格
 * @param r 横坐标
 * @param c 纵坐标
 */
public void dfs(char[][] grid, int r, int c) {
    if (!inArea(grid, r, c)) {return;}

if (grid[r][c] != '1') {return;}

grid[r][c] = '2';

dfs(grid, r + 1, c);
    dfs(grid, r - 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}
```

#### 扩展题目

##### 不同岛屿的个数

> 题目来源：[860. 不同岛屿的个数](https://www.lintcode.com/problem/860)。

###### 题目

描述

给定一个由0和1组成的非空的二维网格，一个**岛屿**是指四个方向（包括横向和纵向）都相连的一组1（1表示陆地）。你可以假设网格的四个边缘都被水包围。

找出所有**不同**的岛屿的个数。如果一个岛屿与另一个岛屿形状相同（不考虑旋转和翻折），我们认为这两个岛屿是相同的。

注意：

```
11
1
```

和

```
 1
11
```

是不同的岛屿，因为我们不考虑旋转和翻折。

样例

**样例 1:**

```
输入:
  [
    [1,1,0,0,1],
    [1,0,0,0,0],
    [1,1,0,0,1],
    [0,1,0,1,1]
  ]
输出: 3
解释: 
  11   1    1
  1        11   
  11
   1  
```

**样例 2:**

```
输入: 
  [
    [1,1,0,0,0],
    [1,1,0,0,0],
    [0,0,0,1,1],
    [0,0,0,1,1]
  ]
输出: 1
```

###### 问题分析

1. 该题目在原来求 **岛屿数量** 的基础上记录 **岛屿的路径**，然后对岛屿的路径进行 **标准化**，最后统计不同的岛屿数量即可。

###### 参考代码

~~~java
/**
 * 860. 不同岛屿的个数
 * @param grid: 网格
 * @return: 不同岛屿的个数
 */
Set<String> pathSet = new HashSet<>();  // 存储不同岛屿的路径
StringBuffer pathTemp = new StringBuffer();
int xDelta = -1, yDelta = -1;  // 岛屿坐标相比于基准坐标 (0, 0) 的偏移量，用于岛屿坐标的标准化
public int numberofDistinctIslands(int[][] grid) {
    int res = 0;
    for (int i = 0; i < grid.length; i++) {
        for (int j = 0; j < grid[i].length; j++) {
            if (grid[i][j] == 1) {
                dfs(grid, i, j);
                if (!pathSet.contains(pathTemp.toString())) {  // 不同的岛屿
                    pathSet.add(pathTemp.toString());
                    res++;
                }
                pathTemp = new StringBuffer();
            }
        }
    }
    return res;
}

/**
 * 网格深度优先遍历
 * @param grid  网格
 * @param r 横坐标
 * @param c 纵坐标
 */
public void dfs(int[][] grid, int r, int c) {
    if (!inArea(grid, r, c)) {return;}
    if (grid[r][c] != 1) {return;}
    
    if (pathTemp.length() == 0) {
        pathTemp.append(String.format("%s_%s ", 0, 0));
        xDelta = r;
        yDelta = c;
    }
    else {
        pathTemp.append(String.format("%s_%s ", r - xDelta, c - yDelta));
    }
    grid[r][c] = 2;
    
    dfs(grid, r - 1, c);
    dfs(grid, r, c + 1);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
}

/**
 * 判断点 (r, c) 是否在网格范围内
 * @param grid  网格
 * @param r 横坐标
 * @param c 纵坐标
 * @return  (r, c) 是否在网格范围内
 */
public boolean inArea(int[][] grid, int r, int c) {
    return r >= 0 && r < grid.length && c >= 0 && c < grid[0].length;
}
~~~

### 岛屿的最大面积

#### 题目

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

**示例 1:**

```txt
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
```

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

**示例 2:**

```txt
[[0,0,0,0,0,0,0,0]]
```

对于上面这个给定的矩阵, 返回 0。

**注意:** 给定的矩阵 grid 的长度和宽度都不超过 50。

#### 问题分析

1. 这道题目只需**对每个岛屿做 DFS 遍历**，**求出每个岛屿的面积**就可以了。
2. 求岛屿面积的方法也很简单，代码如下，每遍历到一个格子，就把面积加 1：

```java
   /**
    * 采用 DFS 遍历求陆地所在岛屿的面积
    * @param grid  岛屿数组
    * @param r 陆地横坐标
    * @param c 陆地纵坐标
    * @return  陆地所在岛屿的面积
    */
   public int dfs(int[][] grid, int r, int c) {
       //  base case
       //  如果坐标（r, c）超出岛屿范围，直接返回 0
       if (!inArea(grid, r, c)) {
           return 0;
       }
   
       //  如果当前格子不是 未遍历陆地，则直接返回 0
       if (grid[r][c] != 1) {
           return 0;
       }
       //  将当前陆地标记为 已遍历陆地
       grid[r][c] = 2;
   
       //  访问上、下、左、右四个相邻接点
       return 1 + dfs(grid, r - 1, c)
               + dfs(grid, r + 1, c)
               + dfs(grid, r, c - 1)
               +dfs(grid, r, c + 1);
   }
   ```

#### 参考代码

```java
/**
 * 判断陆地是否超出岛屿范围
 * @param grid  岛屿数组
 * @param r 陆地横坐标
 * @param c 陆地纵坐标
 * @return  陆地是否超出岛屿范围
 */
public boolean inArea(int[][] grid, int r, int c) {
    return r >= 0 && r < grid.length
            && c >= 0 && c < grid[0].length;
}

/**
 * 采用 DFS 遍历求陆地所在岛屿的面积
 * @param grid  岛屿数组
 * @param r 陆地横坐标
 * @param c 陆地纵坐标
 * @return  陆地所在岛屿的面积
 */
public int dfs(int[][] grid, int r, int c) {
    //  base case
    //  如果坐标（r, c）超出岛屿范围，直接返回 0
    if (!inArea(grid, r, c)) {
        return 0;
    }

//  如果当前格子不是 未遍历陆地，则直接返回 0
    if (grid[r][c] != 1) {
        return 0;
    }
    //  将当前陆地标记为 已遍历陆地
    grid[r][c] = 2;

//  访问上、下、左、右四个相邻接点
    return 1 + dfs(grid, r - 1, c)
            + dfs(grid, r + 1, c)
            + dfs(grid, r, c - 1)
            +dfs(grid, r, c + 1);
}

/**
 * 695. 岛屿的最大面积
 * @param grid  岛屿数组
 * @return  岛屿的最大面积
 */
public int maxAreaOfIsland(int[][] grid) {
    int res = 0;
    for (int i = 0; i < grid.length; i++) {
        for (int j = 0; j < grid[i].length; j++) {
            if (grid[i][j] == 1) {
                int a = dfs(grid, i, j);
                res = Math.max(res, a);
            }
        }
    }
    return res;
}
```

#### 扩展题目

##### [最大正方形](https://leetcode-cn.com/problems/maximal-square)

###### 问题分析

1. 该题目也属于**网格中寻找最值**类型的题目，可以用**DFS**来实现，也可以用**动态规划**来实现，本文选择的是动态规划的方式来实现。
2. 该题目中 $dp$ 数组的含义为 $dp[i][j]$**表示以点 $matrix[i][j]$ 为起点的只包含 `'1'` 的最大正方形的面积**，且：

$$
   dp\lbrack i\rbrack\lbrack j\rbrack=\left\{\begin{array}{lc}0&matrix\lbrack i\rbrack\lbrack j\rbrack='0'\\min(dp\lbrack i\rbrack\lbrack j\;+\;1\rbrack,\;dp\lbrack i\;+\;1\rbrack\lbrack j\;+\;1\rbrack,\;dp\lbrack i\;+\;1\rbrack\lbrack j\rbrack)&matrix\lbrack i\rbrack\lbrack j\rbrack='1'\end{array}\right.
   $$

###### 参考代码

```java
/**
 * 221. 最大正方形
 *
 * @param matrix 二维矩阵
 * @return 二维矩阵中只包含 '1' 的最大正方形的面积
 */
public int maximalSquare(char[][] matrix) {
    int m = matrix.length;
    int n = (m >= 1 ? matrix[0].length : 0);
    //  dp 数组，其中 dp[i][j] 表示以 matrix[i][j] 为起点的只包含 '1' 的最大正方形的面积
    int[][] dp = new int[m + 1][n + 1];
    int res = 0;

for (int i = m - 1; i >= 0; i--) {
        for (int j = n - 1; j >= 0; j--) {
            //  base case
            //  对矩阵右下角的元素进行初始化
            if (matrix[i][j] == '0') {
                dp[i][j] = 0;
            } else if (
                    (i == m - 1 && j == n - 1) ||
                    (i == m - 2 && j == n - 1) ||
                    (i == m - 1 && j == n - 2)
            ) {dp[i][j] = 1;}
            else {

//  分别以当前点 matrix[i][j] 的左边（matrix[i][j + 1]）、对角线（matrix[i + 1][j + 1]）、下边（matrix[i + 1][j]）为起点的只包含 '1' 的最大正方形的面积的的最小值
                int min = Math.min(
                        Math.min(dp[i][j + 1], dp[i + 1][j + 1]),
                        dp[i + 1][j]
                );
                //  dp[i][j] 等于上面求得的最大面积的最小值对应边长加 1 后对应的正方形的面积
                dp[i][j] = (int) Math.pow(Math.sqrt(min) + 1, 2);
            }

//  res 等于 dp[i][j] 中的最大值
            res = Math.max(res, dp[i][j]);
        }
    }

//  返回最后结果
    return res;
}
```

### 填海造陆问题

#### 题目

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的 1 形成。

** 示例 1:**

```txt
输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格 0 变成 1，最终连通两个小岛得到面积为 3 的岛屿。
```

**示例 2:**

```txt
输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格 0 变成 1，岛屿的面积扩大为 4。
```

**示例 3:**

```txt
输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有 0 可以让我们变成 1，面积依然为 4。
```

**提示：**

* n == grid.length
* n == grid[i].length
* 1 <= n <= 500
* grid[i][j] 为 0 或 1

#### 问题分析

1. 这道题是[岛屿最大面积问题](#4-1-岛屿的最大面积)的升级版，现在我们有填海造陆的能力，可以**把一个海洋格子变成陆地格子**，进而**让两块岛屿连成一块**，然后求出**填海造陆之后最大可能构成的岛屿的最大面积**。
2. 我们可以**先计算出所有岛屿的面积**，**然后在所有的格子上标记出岛屿的最大面积**，**最后搜索出哪个海洋格子相邻的两个岛屿面积最大**。
3. 例如下图中红色方框内的海洋格子，上边、左边都与岛屿相邻，我们可以计算出他变成陆地之后可以连接成的岛屿面积为 7 + 1 + 2 = 10。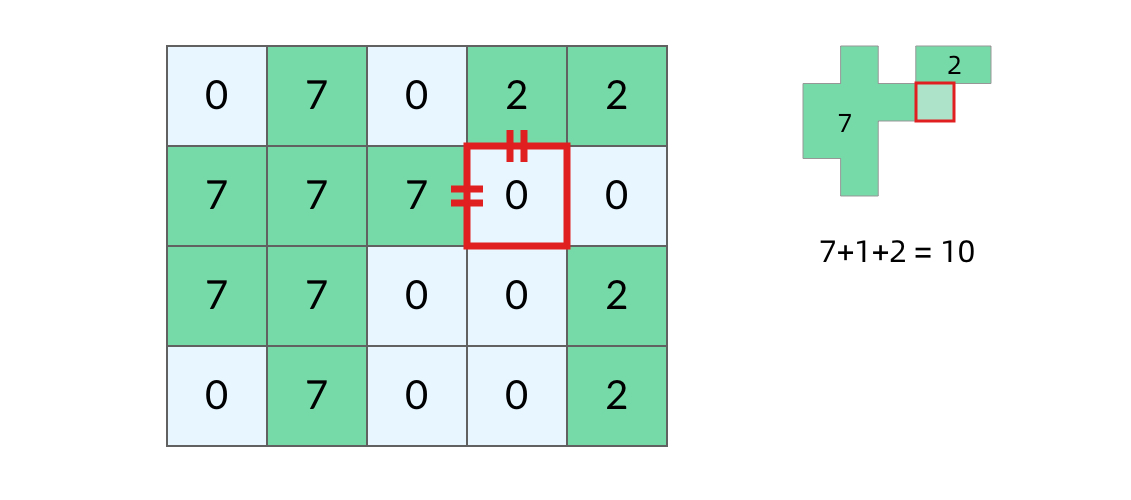![一个海洋格子连接起两个岛屿](https://notebook.ricear.com/media/202107/2021-07-04_201432.png)
4. 然而，这种做法可能遇到一个问题，如下图中红色方框内的海洋格子，他的上边、左边都与岛屿相邻，这时候连接成的岛屿面积并不是 7 + 1 + 7，因为**这两个 7 来自同一个岛屿**，所以填海造陆之后得到的岛屿面积应该只有 7 + 1 = 8。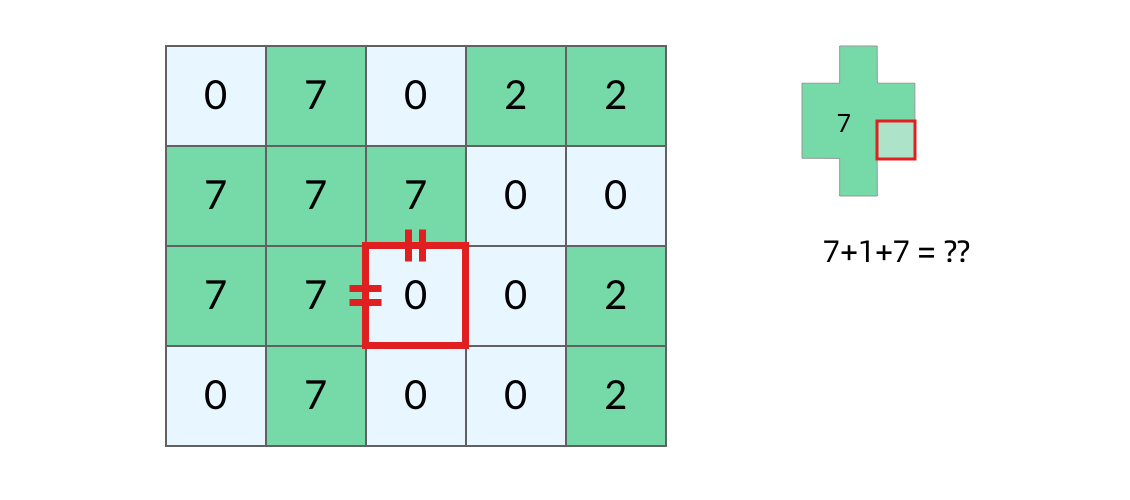![一个海洋格子与同一个岛屿有两个边相邻](https://notebook.ricear.com/media/202107/2021-07-04_201718.png)
5. 可以看到，要让算法正确，我们需要**区分一个海洋格子相邻的 7 是不是来自同一个岛屿**，那么我们可以**不在方格中标记岛屿的面积**，**而应该标记岛屿的索引**（下标），另外**用一个数组记录每个岛屿的面积**，如下图所示，这样我们就可以发现**红色方框内的海洋格子的两个相邻岛屿实际上是一个**。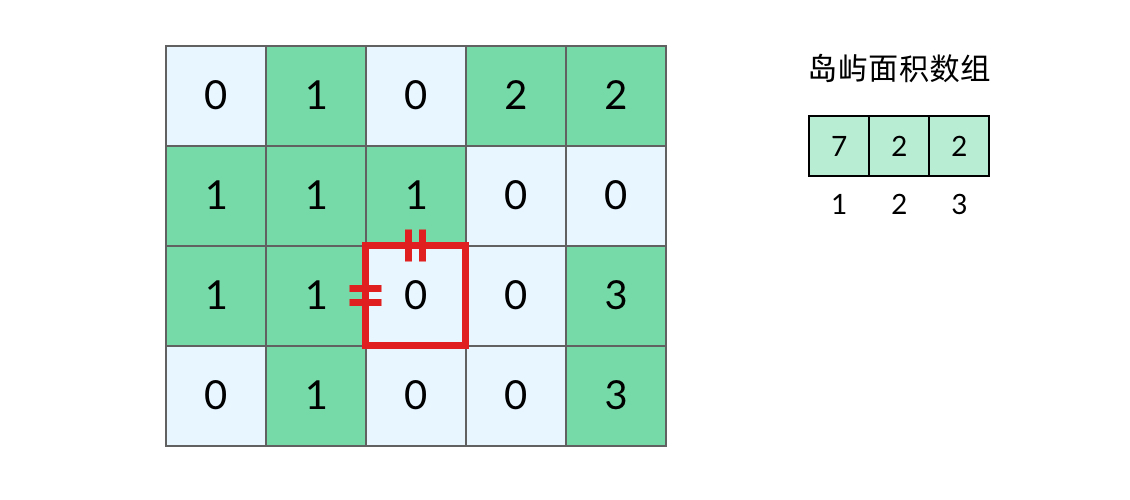![标记每个岛屿的索引（下标）](https://notebook.ricear.com/media/202107/2021-07-04_202139.png)
6. 可以看到，这道题实际上**对网络做了两遍 DFS**：
   1. **第一遍 DFS 遍历陆地格子**，**计算每个岛屿的面积并标记岛屿**。
   2. **第二遍 DFS 遍历海洋格子**，**观察每个海洋格子相邻的陆地格子**。
7. 这道题的基本思路就是这样，具体的代码还有一些需要注意的细节，但和本文的主题已经联系不大，这个会在后面有时间的时候在完善具体的代码实现。

### 岛屿的周长

#### 题目

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

**示例 1：**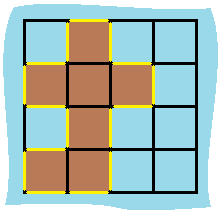

![](https://notebook.ricear.com/media/202108/2021-08-15_1935140.4830911464461979.png)

```txt
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边
```

**示例 2：**

```txt
输入：grid = [[1]]
输出：4
```

**示例 3：**

```txt
输入：grid = [[1,0]]
输出：4
```

**提示：**

* row == grid.length
* col == grid[i].length
* 1 <= row, col <= 100
* grid[i][j] 为 0 或 1

#### 问题分析

1. 实际上，**岛屿的周长是计算岛屿全部的边缘**，而**这些边缘就是我们在 DFS 遍历中 `dfs` 函数返回的位置**。
2. 我们可以将岛屿的周长分为两类：

1. **与网格边界相邻的周长：**`dfs` 函数因为**坐标 $(r,c)$ 超出网格范围而返回的时候就经过了一条相应的边**。
   2. **与海洋格子相邻的周长：**`dfs` 函数因为**当前格子是海洋格子而返回的时候就经过了一条相应的边**。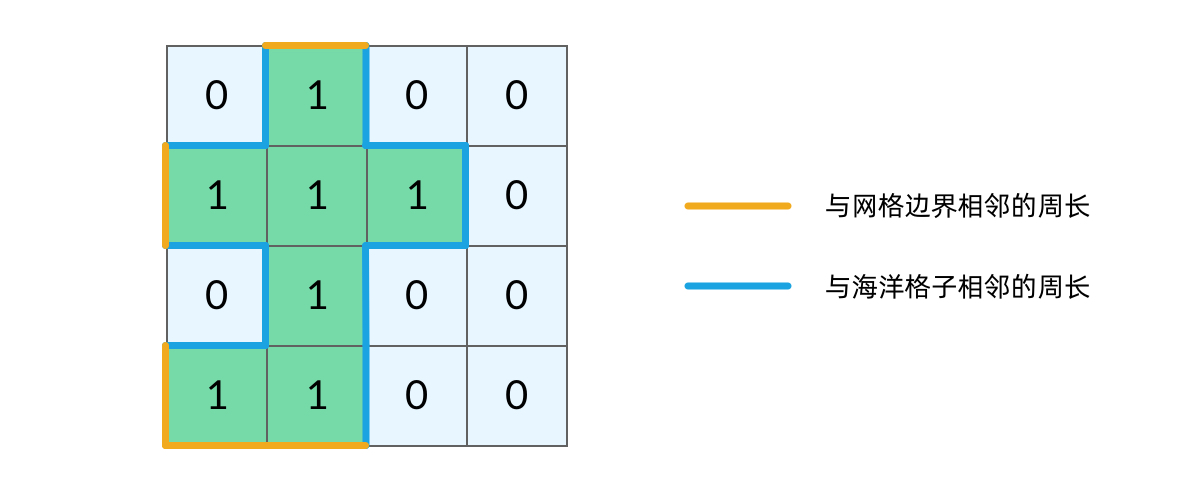![将岛屿周长中的边分为两类](https://notebook.ricear.com/media/202108/2021-08-15_1936420.45840867566908317.png)
3. 这样，我们就**把岛屿周长和 DFS 遍历联系起来了**，具体的代码如下：

```java
   /**
    * 采用 DFS 遍历求陆地所在岛屿的周长
    * @param grid  岛屿数组
    * @param r 陆地横坐标
    * @param c 陆地纵坐标
    * @return  陆地所在岛屿的面积
    */
   public int dfs(int[][] grid, int r, int c) {
       //  base case
       //  坐标（r, c）超出岛屿范围，对应一条 与网格边界相邻的边
       if (!inArea(grid, r, c)) {
           return 1;
       }
   
       //  当前格子是 海洋格子，对应一条 与海洋格子相邻的边
       if (grid[r][c] == 0) {
           return 1;
       }
   
       //  当前格子是 已遍历陆地，与 周长 无关
       if (grid[r][c] != 1) {
           return 0;
       }
       //  将当前陆地标记为 已遍历陆地
       grid[r][c] = 2;
   
       //  访问上、下、左、右四个相邻接点
       return dfs(grid, r - 1, c)
               + dfs(grid, r + 1, c)
               + dfs(grid, r, c - 1)
               +dfs(grid, r, c + 1);
   }
   ```

#### 参考代码

```java
/**
 * 判断陆地是否超出岛屿范围
 * @param grid  岛屿数组
 * @param r 陆地横坐标
 * @param c 陆地纵坐标
 * @return  陆地是否超出岛屿范围
 */
public boolean inArea(int[][] grid, int r, int c) {
    return r >= 0 && r < grid.length
            && c >= 0 && c < grid[0].length;
}

/**
 * 采用 DFS 遍历求陆地所在岛屿的周长
 * @param grid  岛屿数组
 * @param r 陆地横坐标
 * @param c 陆地纵坐标
 * @return  陆地所在岛屿的面积
 */
public int dfs(int[][] grid, int r, int c) {
    //  base case
    //  坐标（r, c）超出岛屿范围，对应一条 与网格边界相邻的边
    if (!inArea(grid, r, c)) {
        return 1;
    }

//  当前格子是 海洋格子，对应一条 与海洋格子相邻的边
    if (grid[r][c] == 0) {
        return 1;
    }

//  当前格子是 已遍历陆地，与 周长 无关
    if (grid[r][c] != 1) {
        return 0;
    }
    //  将当前陆地标记为 已遍历陆地
    grid[r][c] = 2;

//  访问上、下、左、右四个相邻接点
    return dfs(grid, r - 1, c)
            + dfs(grid, r + 1, c)
            + dfs(grid, r, c - 1)
            +dfs(grid, r, c + 1);
}

/**
 * 463. 岛屿的周长
 * @param grid  岛屿
 * @return  岛屿的周长
 */
public int islandPerimeter(int[][] grid) {
    for (int i = 0; i < grid.length; i++) {
        for (int j = 0; j < grid[i].length; j++) {
            if (grid[i][j] == 1) {
                //  题目限制只有一个岛屿，计算一个即可
                return dfs(grid, i, j);
            }
        }
    }
    return -1;
}
```

### [单词搜索](https://leetcode-cn.com/problems/word-search)

#### 题目

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

**示例 1：**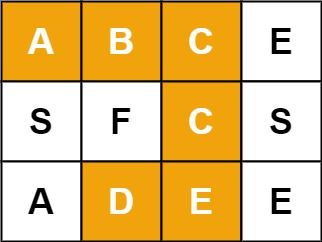

![](https://notebook.ricear.com/media/202108/2021-08-28_1951260.6416354552062601.png)

```txt
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
```

**示例 2：**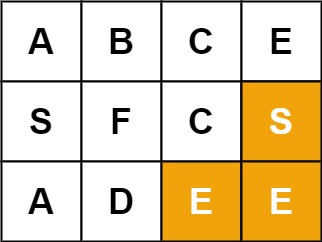

![](https://notebook.ricear.com/media/202108/2021-08-28_1951340.03564141591250025.png)

```txt
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true
```

**示例 3：**

![](https://notebook.ricear.com/media/202108/2021-08-28_1951460.9733885442865199.png)

```txt
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false
```

**提示：**

* m == board.length
* n = board[i].length
* 1 <= m, n <= 6
* 1 <= word.length <= 15
* board 和 word 仅由大小写英文字母组成

**进阶：** 你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

#### 问题分析

1. 该题目为**网格搜索**类题目，可以利用**网格 DFS**的框架来解决。
2. 需要注意的是，该题目在遍历的时候**涉及到回退的操作**，因此**需要建立一个数组**，用来**标记当前节点是否使用过**，**如果使用过则直接跳过**，但是最后**如果当前遍历得到的字符串和原来的字符串不相等**，**需要进行回退**，**把刚才标记为使用过的节点标记为未使用**，**相当于原来的节点没有使用**。

#### 参考代码

```java
//  最后结果
boolean res = false;

/**
 * 79. 单词搜索
 * @param board 二维字符网格
 * @param word  字符串单词
 * @return  字符串单词是否存在于二维字符网络中
 */
public boolean exist(char[][] board, String word) {
    int index = 0;

for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[i].length; j++) {
            int[][] used = new int[board.length][board[i].length];
            dfs(board, word, i, j, index, used);
            if (res) {return true;}
        }
    }

return false;
}

/**
 * 深度优先遍历判断字符串单词是否存在于二维字符网络中
 * @param board 二维字符网格
 * @param word  字符串单词
 * @param i 当前遍历的二维字符网络中字符的横坐标
 * @param j 当前遍历的二维字符网络中字符的纵坐标
 * @param index 当前遍历的字符串单词的下标
 * @param used  当前遍历的二维字符网络中字符是否使用过
 */
public void dfs(char[][] board, String word, int i, int j, int index, int[][] used) {
    if (!inArea(board, word, i, j, index, used)) {return;}

if (index == word.length() - 1 && board[i][j] == word.charAt(index) && used[i][j] != -1) {
        res = true;
        return;
    }

//  标记当前字符为已经使用过
    used[i][j] = -1;

if (!res) {dfs(board, word, i, j + 1, index + 1, used);}
    if (!res) {dfs(board, word, i + 1, j, index + 1, used);}
    if (!res) {dfs(board, word, i, j - 1, index + 1, used);}
    if (!res) {dfs(board, word, i - 1, j, index + 1, used);}
    if (!res) {
        //  如果字符串单词不在于二维字符网络中，则撤销原来的标记
        used[i][j] = 0;
    }
}

/**
 * 判断当前遍历的二维字符网络中字符是否在边界内
 * @param board 二维字符网格
 * @param word  字符串单词
 * @param i 当前遍历的二维字符网络中字符的横坐标
 * @param j 当前遍历的二维字符网络中字符的纵坐标
 * @param index 当前遍历的字符串单词的下标
 * @param used  当前遍历的二维字符网络中字符是否使用过
 * @return  判断当前遍历的二维字符网络中字符是否在边界内
 */
public boolean inArea(char[][] board, String word, int i, int j, int index, int[][] used) {
    if ((i < 0 || i >= board.length || j < 0 || j >= board[i].length)) {return false;}
    if (index < 0 || index >= word.length()) {return false;}
    if (used[i][j] == -1) {return false;}
    if (board[i][j] != word.charAt(index)) {return false;}
    return true;
}
```

### [机器人的运动范围](https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof)

#### 题目

地上有一个 m 行 n 列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如，当 k 为 18 时，机器人能够进入方格 [35, 37] ，因为 3+5+3+7=18。但它不能进入方格 [35, 38]，因为 3+5+3+8=19。请问该机器人能够到达多少个格子？

**示例 1：**

```txt
输入：m = 2, n = 3, k = 1
输出：3
```

**示例 2：**

```txt
输入：m = 3, n = 1, k = 0
输出：1
```

**提示：**

* 1 <= n,m <= 100
* 0 <= k <= 20

#### 问题分析

1. 该题目为**网格搜索**类题目，可以利用**网格 DFS**的框架来解决。

#### 参考代码

```java
/**
 * 计算机器人当前位置的横纵坐标数位之和
 * @param i 横坐标
 * @param j 纵坐标
 * @return  机器人当前位置的横纵坐标数位之和
 */
public int calculate(int i, int j) {
    String tmp = String.valueOf(i) + String.valueOf(j);
    char[] arr = tmp.toCharArray();
    int sum = 0;
    for (char c: arr) {
        sum += c - '0';
    }
    return sum;
}

/**
 * 判断机器人是否在方格内
 * @param grid  方格
 * @param i 横坐标
 * @param j 纵坐标
 * @param k 横坐标和列坐标的最大数位之和
 * @return  机器人是否在方格内
 */
public boolean inArea(int[][] grid, int i, int j, int k) {
    return i >= 0 && i < grid.length && j >= 0 && j < grid[i].length && calculate(i, j) <= k;
}

/**
 * 深度优先遍历计算机器人在当前位置能够到达的最大格子数
 * @param grid  方格
 * @param r 机器人的横坐标
 * @param c 机器人的纵坐标
 * @param k 横坐标和列坐标的最大数位之和
 * @param used  当前位置是否遍历过
 * @return  机器人在当前位置能够到达的最大格子数
 */
public int dfs(int[][] grid, int r, int c, int k, boolean[][] used) {
    if (!inArea(grid, r, c, k)) {return 0;}
    if (used[r][c]) {return 0;}

//  标记当前位置已经使用过
    used[r][c] = true;

return 1 + dfs(grid, r - 1, c, k, used) + dfs(grid, r, c + 1, k, used) + dfs(grid, r + 1, c, k, used) + dfs(grid, r, c - 1, k, used);
}

/**
 * 剑指 Offer 13. 机器人的运动范围
 * @param m 行数
 * @param n 列数
 * @param k 横坐标和列坐标的最大数位之和
 * @return  机器人能够到达的最大格子数
 */
public int movingCount(int m, int n, int k) {
    int[][] grid = new int[m][n];
    boolean[][] used = new boolean[m][n];
    int res = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            res = Math.max(res, dfs(grid, i, j, k, used));
        }
    }
    return res;
}
```

## 参考文献

1. [岛屿类问题的通用解法、DFS 遍历框架](https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-lei-wen-ti-de-tong-yong-jie-fa-dfs-bian-li-)。