🧮 Algorithm Notebook
1、算法准备
1.1 牛客网编程OJ的典型输入输出
2、算法框架
2.1 动态规划
2.1.1 斐波那契数列
2.1.2 背包问题
2.1.3 贪心算法
2.1.4 序列和数组类问题
2.1.5 编辑距离
2.1.6 高楼扔鸡蛋
2.1.7 股票问题系列通解
2.1.8 最长有效括号
2.1.9 剪绳子
2.1.10 正则表达式匹配
2.2 二分查找
2.2.1 二分查找框架
2.2.2 搜索旋转排序数组
2.3 链表
2.3.1 反转链表
2.3.2 相交链表
2.3.3 合并链表
2.3.4 链表中倒数第k个节点
2.3.5 复制带随机指针的链表
2.4 排序算法
2.4.1 常见排序算法
2.5 二叉树
2.5.1 二叉树遍历
2.5.2 岛屿问题
2.5.3 二叉树路径问题
2.5.4 构造二叉树
2.6 回溯算法
2.6.1 回溯算法解题框架
2.6.2 N皇后
2.7 数组
2.7.1 删除有序数组中的重复项
2.7.2 滑动窗口最大值
2.7.3 调整数组顺序使奇数位于偶数前面
2.7.4 螺旋矩阵
2.7.5 多数元素
2.7.6 最大数
2.7.7 和为s的两个数字
2.7.8 构建乘积数组
2.7.9 两数之和
2.8 字符串
2.8.1 最小覆盖子串
2.8.2 比较版本号
2.8.3 验证IP地址
2.8.4 基本计算器 II
2.8.5 字符串解码
2.8.6 移掉 K 位数字
2.8.7 无重复字符的最长子串
2.8.8 第一个只出现一次的字符
2.8.9 翻转字符串里的单词
2.8.10 字符串转换整数 (atoi)
2.8.11 字符串四则运算
2.9 栈
2.9.1 最小栈
2.9.2 弹出序列
2.10 数学
2.10.1 用 Rand7() 实现 Rand10()
2.10.2 只出现一次的数字
2.10.3 整数反转
2.10.4 求1+2+…+n
2.10.5 二进制中1的个数
2.10.6 幂运算
2.10.7 1~n 整数中 1 出现的次数
2.10.8 数字序列中某一位的数字
2.10.9 丑数
2.10.10 n个骰子的点数
2.10.11 圆圈中最后剩下的数字
2.10.12 不用加减乘除做加法
2.10.13 x 的平方根
2.11 设计
2.11.1 LRU 缓存机制
-
+
游客
注册
登录
1~n 整数中 1 出现的次数
## 1 题目 输入一个整数 n ,求 1~n 这 n 个整数的十进制表示中 1 出现的次数。 例如,输入 12,1~12 这些整数中包含 1 的数字有 1、10、11 和 12,1 一共出现了 5 次。 **示例 1:** ```txt 输入:n = 12 输出:5 ``` **示例 2:** ```txt 输入:n = 13 输出:6 ``` **限制:** * 1 <= n < 2^31 ## 2 问题分析 1. **将 $ 1 \sim n$ 的个位**、**十位**、**百位**、...**的 1 出现次数相加**,**即为 1 出现的总次数**。 2. **设数字 $n$ 是个 $x$ 位数**,**记 $n$ 的第 $i$ 位为 $n_i$**,**则可将 $n$ 写为 $n_xn_{x-1} \cdots n_2n_1$**: 1. **称 $n_i$ 为当前位**,**记为 $cur$**。 2. **将 $n_{i-1}n_{i-2} \cdots n_2n_1$ 称为低位**,**记为 $low$**。 3. **将 $n_xn_{x-1} \cdots n_{i+2}n_{i+1}$ 称为高位**,**记为 $high$**。 4. **将 $ 10^i$ 称为位因子**,**记为 $digit$**。 3. 在**计算某位中 1 出现次数时**,**根据当前位 $cur$ 值的不同**,**分为以下三种情况**: 1. **当 $cur = 0$ 时**,**此位 1 的出现次数只由高位 $high$ 决定**,计算公式为: $$ high \times digit $$ 1. **当 $cur = 1$ 时**,**此位 1 的出现次数由高位 $high$ 和低位 $low$ 决定**,计算公式为: $$ high \times digit + low + 1 $$ 2. **当 $cur = 2, 3, ..., 9$ 时**,**此位 1 的出现次数只由高位 $high$ 决定**,计算公式为: $$ (high + 1) \times digit $$ 4. **变量递推公式为**: 1. **设计按照个位**、**十位**、...**的顺序计算**,则 $high / cur / low / digit$**应初始化为**: 1. $high = n / 10$。 2. $cur = n % 10$。 3. $low = 0$。 4. $digit = 1$,即**个位**。 2. 因此,**从个位到最高位的变量递推公式为**: 1. $low += cur * digit$,即**将 $cur$ 加入 $low$**,**组成下轮 $low$**。 2. $cur = high \% 10$,即**下轮 $cur$ 是本轮 $high$ 的最低位**。 3. $high /= 10$,即**将本轮 $high$ 最低位删除**,**得到下轮 $high$**。 4. c$digit *= 10$,即**位因子每轮 $\times$ 10**。 5. 具体实例如下: 1. 当 $cur = 0$ 时,以 $n = 2304$ 为例,求 $digit = 10$(即十位)的 1 出现次数: 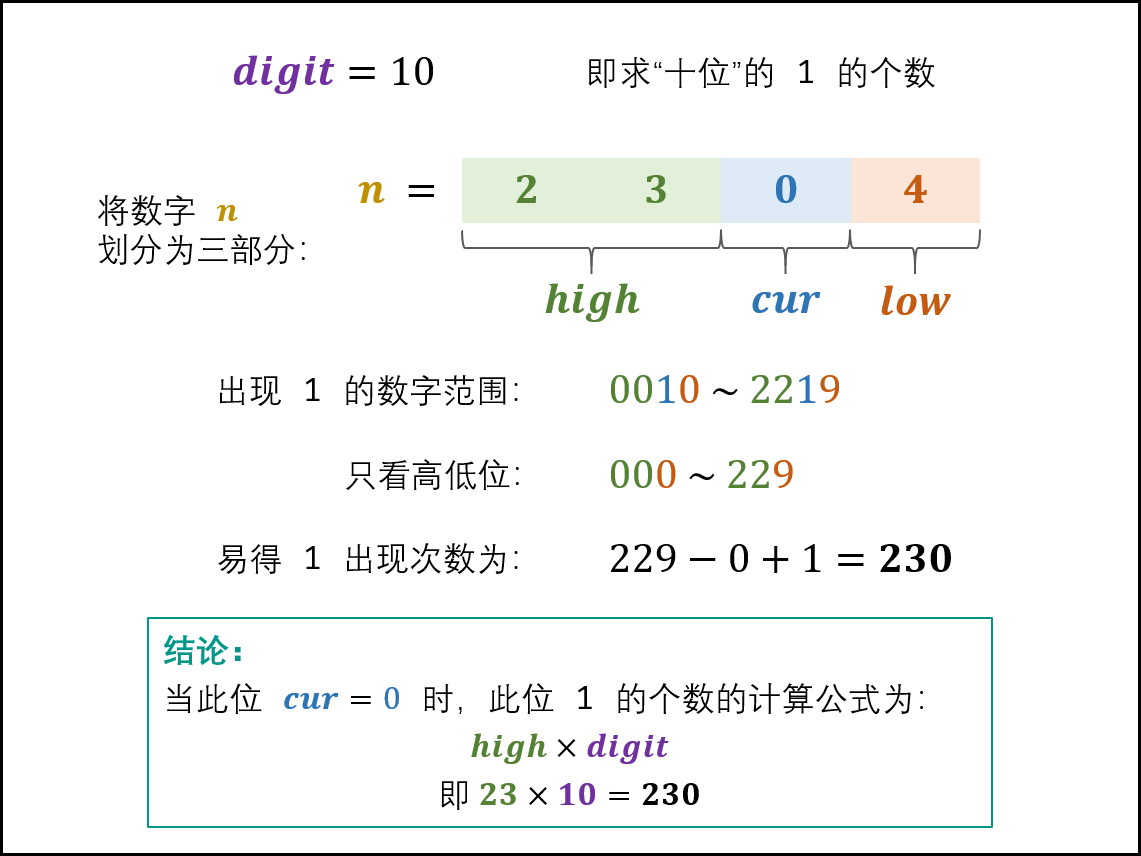 2. 当 $cur = 1$ 时,以 $n = 2314$ 为例,求 $digit = 10$(即十位)的 1 出现次数: 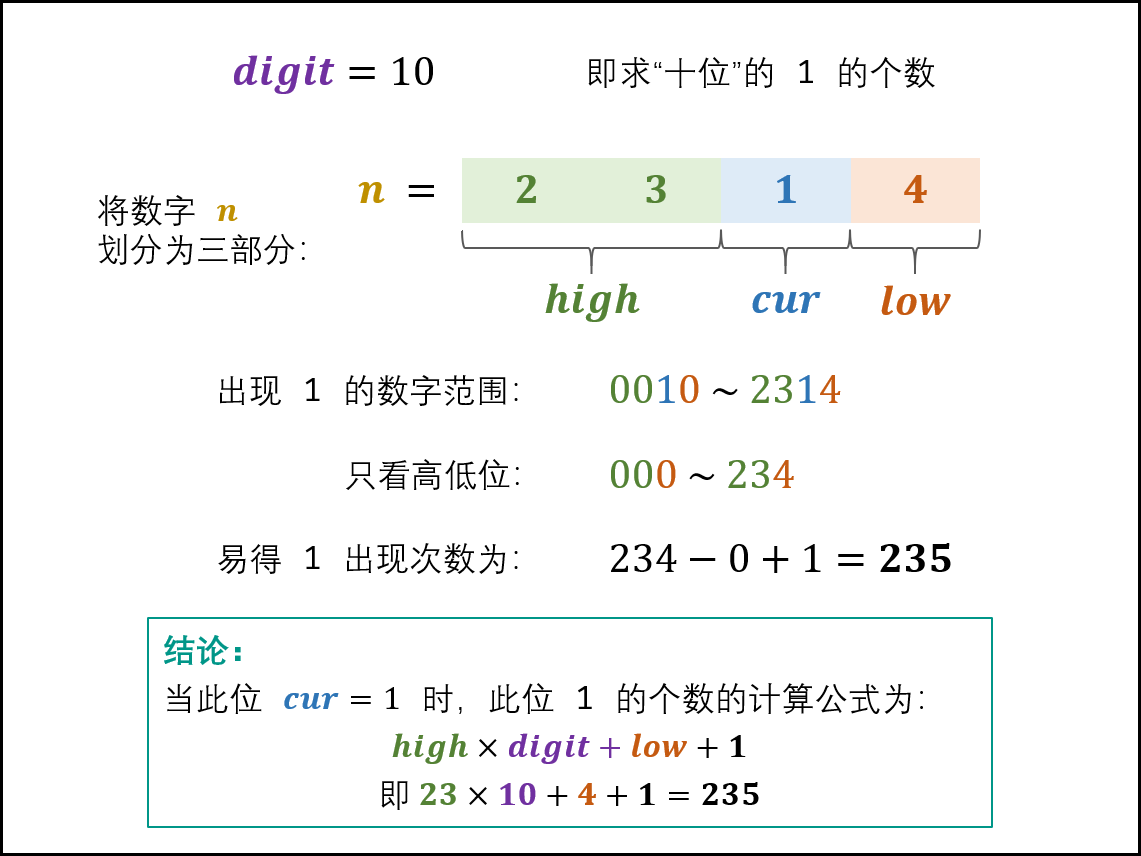 3. 当 $cur = 2, 3, ..., 9$ 时,以 $n = 2324$ 为例,求 $digit = 10$(即十位)的 1 出现次数: 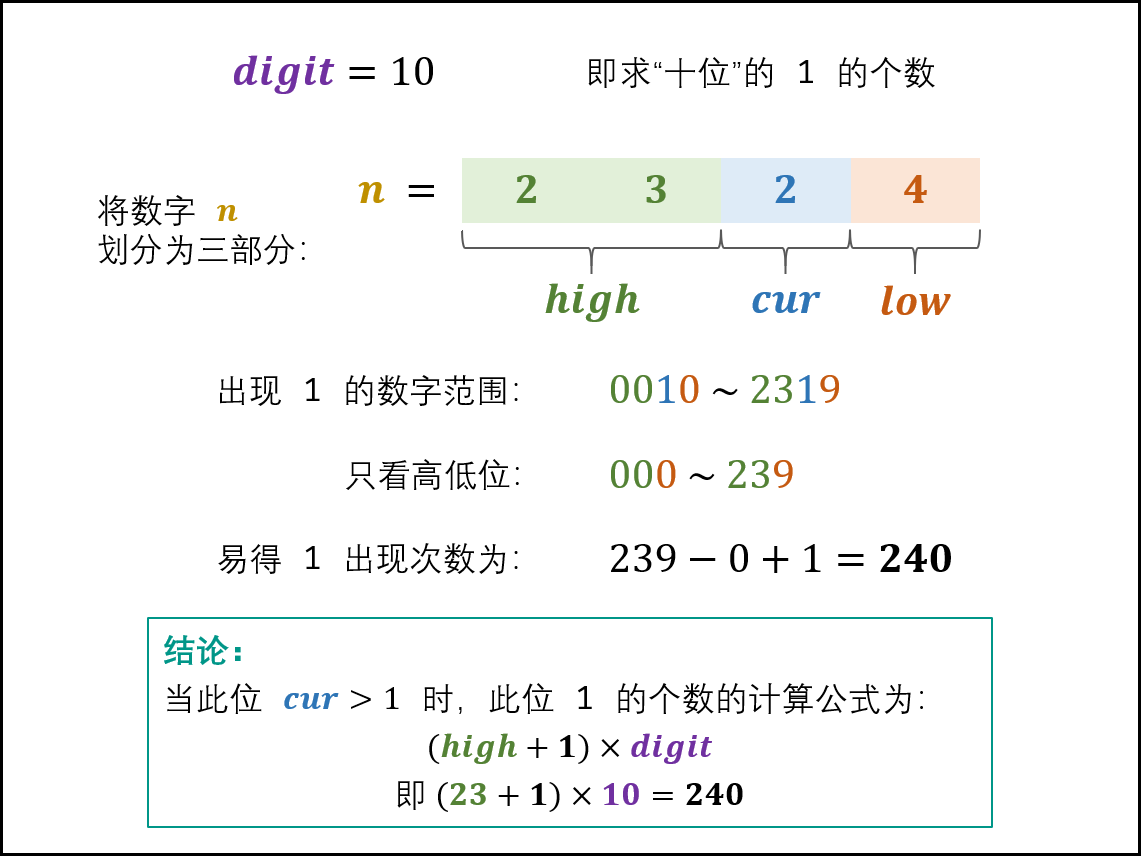 ## 3 参考代码 ```java /** * 剑指 Offer 43. 1~n 整数中 1 出现的次数 * @param n 整数 * @return 1~n 整数中 1 出现的次数 */ public int countDigitOne(int n) { int low = 0, high = n / 10, cur = n % 10, digit = 1, res = 0; while (high != 0 || cur != 0) { // 当 high 和 cur 同时为 0 时,说明已经越过最高位,因此跳出 if (cur == 0) {res += high * digit;} else if (cur == 1) {res += high * digit + low + 1;} else {res += (high + 1) * digit;} // 将 cur 加入 low,组成下轮 low low += cur * digit; // 下轮 cur 是本轮 high 的最低位 cur = high % 10; // 将本轮 high 最低位删除,得到下轮 high high = high / 10; // 位因子每轮 x 10 digit *= 10; } return res; } ``` ## 参考文献 1. [剑指 Offer 43. 1~n 整数中 1 出现的次数](https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof)。 2. [面试题 43. 1~n 整数中 1 出现的次数(清晰图解)](https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/solution/mian-shi-ti-43-1n-zheng-shu-zhong-1-chu-xian-de-2)。
ricear
2022年6月19日 10:42
©
BY-NC-ND(4.0)
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
分享
链接
类型
密码
更新密码