回溯算法解题框架

## 含义

1. 回溯算法**建立在 DFS 基础之上**，与 DFS 的主要不同在于：

1. DFS 是**一个劲的往某一个方向搜索**，**等到到达一个方向的终点时**，才**恢复状态**，**回溯上一层**。
   2. 回溯算法在**达到结束条件后**，就**恢复状态**，**回溯上一层**。
2. 当**问题需要回头**，**以此来查出所有的解的时候**，**使用回溯算法**，即**满足结束条件或者发现不是正确路径的时候**（走不通），**要撤销选择**，**回退到上一个状态**，**继续尝试**，**直到找出所有解为止**。
3. 解决一个回溯算法时主要按照以下步骤：

1. **画出递归树**，**找到状态变量**（回溯函数的参数），这一部非常重要。
   2. **根据题意**，**确定结束条件**。
   3. **找准选择列表**（与函数参数相关），与第一步紧密关联。
   4. **判断是否需要剪枝**。
   5. **做出选择**，**递归调用**，**进入下一层**。
   6. **撤销选择**。
4. 回溯算法的核心就是**for 循环里面的递归**，即**在递归调用之前【做选择】**，**在递归调用之后【撤销选择】**，解题框架如下：

```python
   result = []
   def backtrack(路径, 选择列表):
       if 满足结束条件:
           result.add(路径)
           return
   
       for 选择 in 选择列表:
           做选择
           backtrack(路径, 选择列表)
           撤销选择
   ```

## 应用场景

回溯算法的应用场景主要包括以下几个方面：

1. [子集、组合](#2-1-子集-组合)（$i$**从 $start$ 开始**）：
   1. **子集**：
      1. **没有结束条件**。
   2. **组合**：
      1. **有结束条件**。
2. [全排列](#2-2-1-全排列)（$i$ **从 0 开始**，同时 **添加 $used$ 数组**）：
   1. **数组中的元素互不相同**（处理方式与子集类似）。
   2. **数组中包含重复元素**（处理方式与子集类似）。

> 回溯算法的 **去重**：
>
> 先**对数组排序**，然后**当 `i > 0 && nums[i] == nums[i - 1]` 时跳过**（子集/组合问题去重时的判断是使用 $i \gt start$，全排列去重时的判断是使用 $i \gt 0$）。

> 需要注意的是，**子集**、**组合与排列是不同性质的概念**，**子集**、**组合是无关顺序的**，而**排列是和元素顺序有关的**，例如 `[1, 2]` 和 `[2, 1]` 是同一个组合（子集），但是是两种不一样的排列，因此被分为两类问题。

### 子集、组合

#### 子集

> 题目来源：[78. 子集](https://leetcode.cn/problems/subsets)。

##### 问题分析

1. **递归树**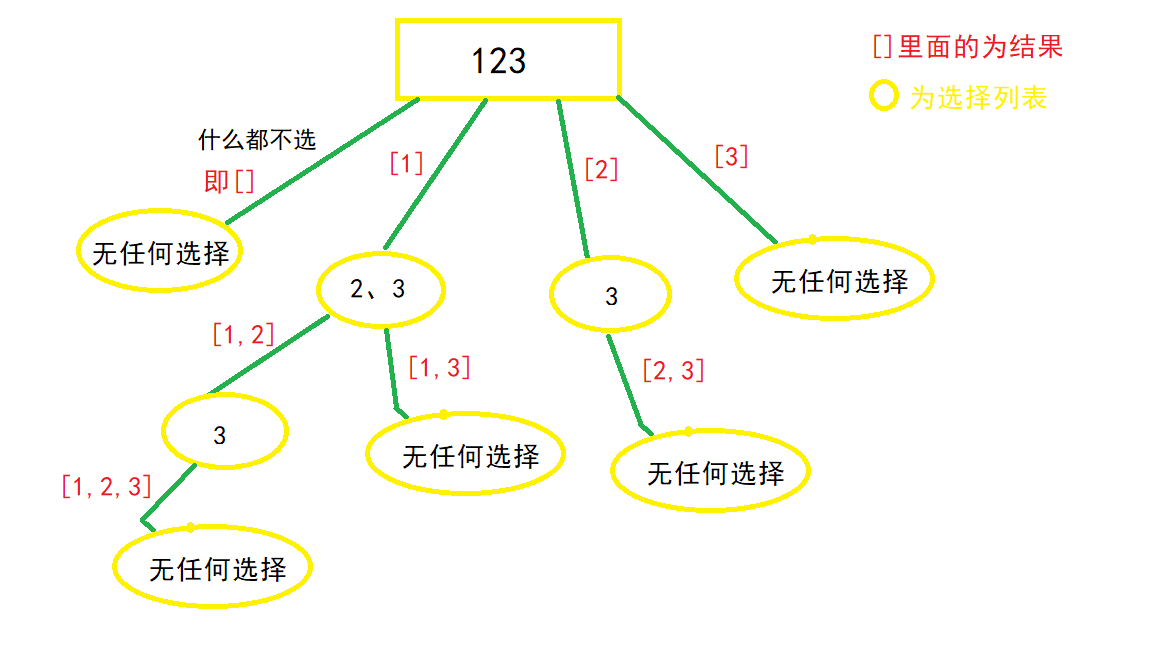：![子集问题递归树.png](https://notebook.ricear.com/media/202108/2021-08-20_1948440.2591370108797909.png)
   1. 观察上图可得**选择列表里的数**，**都是选择路径**（红色框）**后面的数**，比如 `[1]` 这条路径，他后面的选择列表只有 `2、3`，`[2]` 这条路径后面只有 3 这个选择，那么**这个时候**，就**应该使用一个参数 `start`**，**来标识当前的选择列表的起始位置**，**也就是标识每一层的状态**，因为被形象的称为**状态变量**，**最终函数签名如下**：

```java
      // nums 为题目中给的数组
      // track 为路径结果，要把每一条 path 加入结果集
      public void backtrack(int[] nums, LinkedList<Integer> track, int start)
      ```
2. **找结束条件**：
   1. **此题非常特殊**，**所有路径都应该加入结果集**，所以**不存在结束条件**。
   2. **当 `start` 参数越过数组边界的时候**，**程序就自己跳过下一层递归了**，因此**不需要手写结束条件**，**直接加入结果集**：

```java
      // res 为结果集，是全局变量，到时候需要返回
      LinkedList list = new LinkedList<>(track);
      res.add(list);
      ```
3. **找选择列表**：
   1. 在 1 中已经提过，**子问题的选择列表**，**是上一条选择路径之后的数**，即

```java
      for (int i = start; i < nums.length; i++)
      ```
4. **判断是否需要剪枝**：
   1. **从递归树中看到**，**路径没有重复的**，**也没有不符合条件的**，所以**不需要剪枝**。
5. **做出选择**：
   1. 即**将节点添加到路径中**：

```java
      track.add(nums[i]);
      ```
6. **撤销选择**：
   1. 即**将节点从路径中移除**：

```java
      track.removeLast();
      ```

##### 参考代码

```java
//  最后结果
List<List<Integer>> res = new ArrayList<>();

/**
 * 78. 子集
 * @param nums  数组
 * @return  该数组所有可能的子集
 */
public List<List<Integer>> subsets(int[] nums) {
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track, 0);
    return res;
}

/**
 * 回溯法求解子集问题
 * @param nums  数组
 * @param track 路径
 * @param start 起始位置
 */
public void backtrack(int[] nums, LinkedList<Integer> track, int start) {
    //  将路径添加到结果列表中
    LinkedList list = new LinkedList<>(track);
    res.add(list);
    for (int i = start; i < nums.length; i++) {
        //  做选择：将节点添加到路径中
        track.add(nums[i]);
        backtrack(nums, track, i + 1);
        //  撤销选择：将节点从路径中移除
        track.removeLast();
    }
}
```

#### 子集 II

> 题目来源：[90. 子集 II](https://leetcode.cn/problems/subsets-ii)。

##### 问题分析

1. **递归树**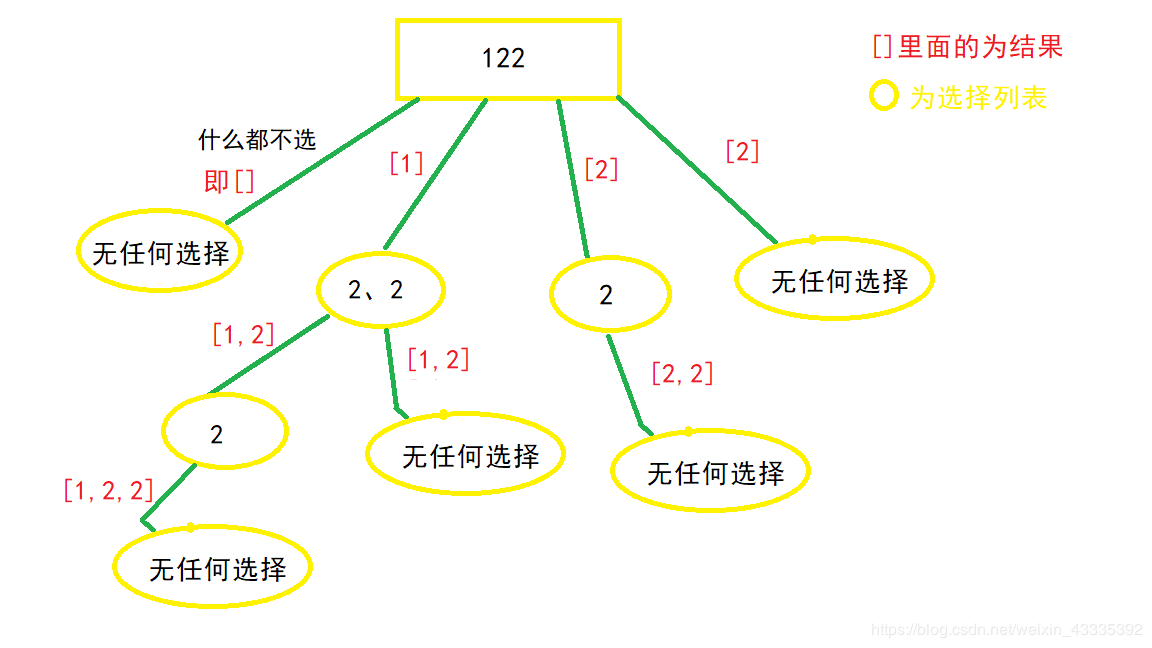：![在这里插入图片描述](https://notebook.ricear.com/media/202108/2021-08-20_2007080.467171720456268.png)
   1. 从图中可以发现，**树中出现了大量重复的集合**，找结束条件和选择列表与[2.1.1 子集](#2-1-1-子集)一样，不再赘述，我们直接看判断是否需要剪枝。
2. **判断是否需要剪枝**
   1. 因为**数组中有重复元素**，而**这些重复元素可能并不在一起**（**回溯算法中时通过数组中前后元素是否一致来判断子集是否重复的**），从而**可能导致后面结果出现重复的子集**，因此**需要先对子集进行排序**，**使得重复的元素都在一起**：

```java
      Arrays.sort(nums);
      ```
   2. 我们**需要取出重复的集合**，即**需要剪枝**，**把递归树上的某些分支减掉**，观察上图不难发现，**应该去除当前选择列表中**，**与上一个数重复的那个数**，**引出的分支**，如 `2、2` 这个选择列表，第二个 `2` 是最后重复的，应该去除这个 `2` 引出的分值，即下图中红色大框中的分支：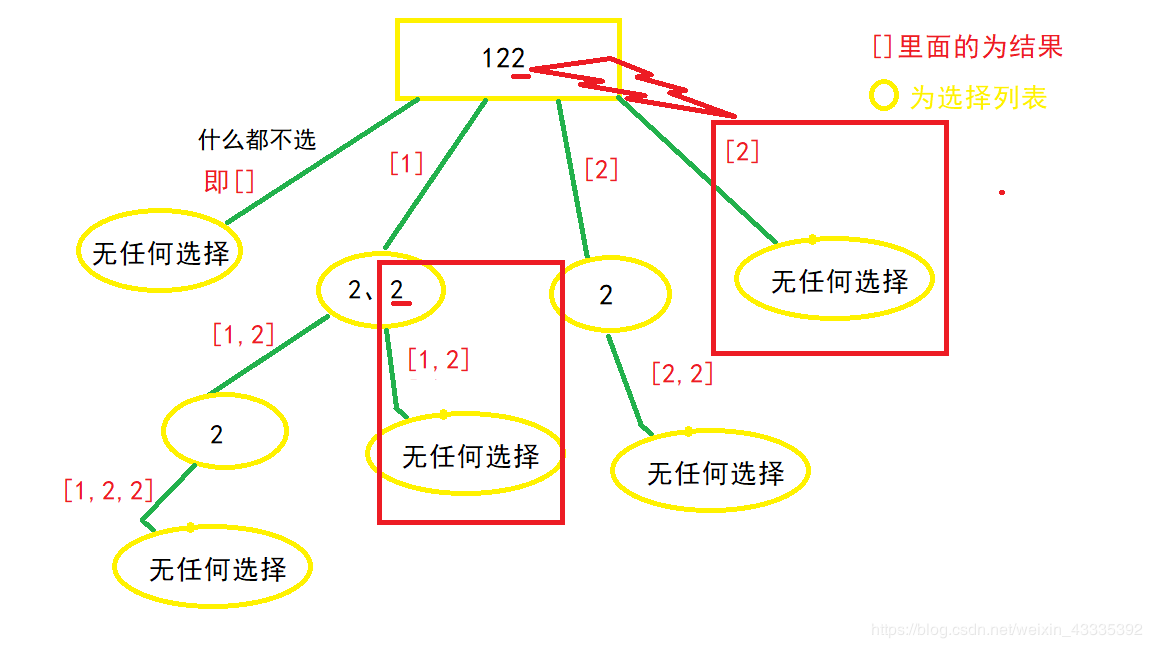

![在这里插入图片描述](https://notebook.ricear.com/media/202108/2021-08-20_2015040.40159480363834765.png)
   3. 因此，在遍历时需要对当前遍历的节点进行判断，如果 $i > start$ 并且 $nums[i] == nums[i - 1]$，那么就需要进行下一个遍历：

```java
      if (i > start && nums[i] == nums[i - 1]) {continue;}
      ```
3. 做出选择和撤销选择与[2.1.1 子集](#2-1-1-子集)一样，这里不再赘述。

##### 参考代码

```java
//  最后结果
List<List<Integer>> res = new ArrayList<>();

/**
 * 90. 子集 II
 * @param nums  数组
 * @return  该数组所有可能的子集
 */
public List<List<Integer>> subsetsWithDup(int[] nums) {
    LinkedList<Integer> track = new LinkedList<>();
    //  因为数组中有重复元素，而这些重复元素可能并不在一起（回溯算法中时通过数组中前后元素是否一致来判断子集是否重复的），从而可能导致后面结果出现重复的子集，因此需要先对子集进行排序，使得重复的元素都在一起
    Arrays.sort(nums);
    backtrack(nums, track, 0);
    return res;
}

/**
 * 回溯法解决子集问题
 * @param nums  数组
 * @param track 路径
 * @param start 起始位置
 */
public void backtrack(int[] nums, LinkedList<Integer> track, int start) {
    LinkedList list = new LinkedList<>(track);
    res.add(list);
    for (int i = start; i < nums.length; i++) {
        if (i > start && nums[i] == nums[i - 1]) {continue;}
        //  做选择：将节点添加到路径中
        track.add(nums[i]);
        backtrack(nums, track, i + 1);
        //  撤销选择：将节点从路径中移除
        track.removeLast();
    }
}
```

#### 组合总和

> 题目来源：[39. 组合总和](https://leetcode.cn/problems/combination-sum)。

##### 问题分析

1. **递归树**（绿色箭头上面的是路径，红色框的为结果，黄色框的为选择列表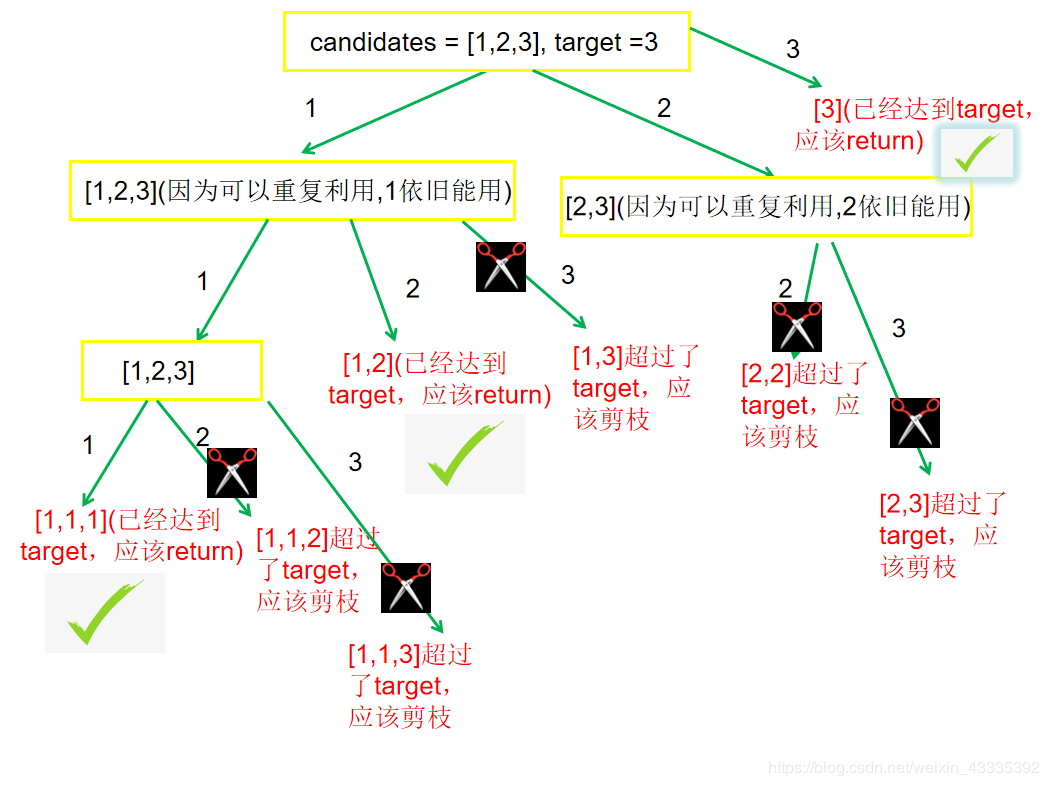）：![在这里插入图片描述](https://notebook.ricear.com/media/202108/2021-08-20_2036250.1406137970451541.png)

1. 从上面可以看出，**组合问题和子集问题一样**，`1、2` 和 `2、1` 是同一个组合，因此**需要引入 `start` 参数标识**，**表示每个状态中选择列表的起始位置**，另外，**每个状态还需要一个 `sum` 变量**，**来记录当前路径的和**，函数签名如下：

```java
      public void backtrack(int[] candidates, LinkedList<Integer> track, int start, int sum, int target)
      ```
2. **找结束条件**：

1. 由题意可得，**当路径总和等于 `target` 的时候**，就应该**把路径加入结果集**，**并返回**，**当路径总和大于 `target` 的时候**，**直接返回**：

```java
      if (sum == target) {
          LinkedList<Integer> list = new LinkedList<>(track);
          res.add(list);
          return;
      }
      if (sum > target) {
          return;
      }
      ```
3. **找选择列表**：

```java
   for (int i = start; i < candidates.length; i++)
   ```
4. **判断是否需要剪枝**：

1. 从 1 中的递归树中发现，**当前状态的 `sum` 大于 `target` 的时候**，**就应该剪枝**，**不用再递归下去了**：

```java
      if (sum > target) {
          return;
      }
      ```
5. **做出选择**：

1. 题目中说**可以无限次被选择**，那么 `i`**就不用 `+1`**，即**下一层的选择列表**，**从自身开始**，并且**需要更新当前状态的 `sum`**：

```java
      track.add(candidates[i]);
      backtrack(candidates, track, i, sum + candidates[i], target);
      ```
6. **撤销选择**：

```java
   track.removeLast();
   ```

##### 参考代码

```java
//  最后结果
List<List<Integer>> res = new ArrayList<>();

/**
 * 39. 组合总和
 *
 * @param candidates 数组
 * @param target     目标和
 * @return candidates 中所有可以使数字和为目标数 target 的唯一组合
 */
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    LinkedList<Integer> list = new LinkedList<>();
    backtrack(candidates, list, 0, 0, target);
    return res;
}

/**
 * 回溯法求解组合总和问题
 *
 * @param candidates 数组
 * @param track      路径
 * @param start      起始位置
 * @param sum        路径中的元素和
 * @param target     目标和
 */
public void backtrack(int[] candidates, LinkedList<Integer> track, int start, int sum, int target) {
    /**
     * 判断结束条件:
     *  如果当前路径中元素和与目标和相等，则将路径添加到结果列表中
     *  如果当前路径中元素和大于目标和，则直接返回
     */
    if (sum == target) {
        LinkedList<Integer> list = new LinkedList<>(track);
        res.add(list);
        return;
    }
    if (sum > target) {
        return;
    }

for (int i = start; i < candidates.length; i++) {
        //  做选择：将节点添加到路径中
        track.add(candidates[i]);
        backtrack(candidates, track, i, sum + candidates[i], target);
        //  撤销选择：将节点从路径中移除
        track.removeLast();
    }
}
```

##### 相关题目

###### 组合总和 II

> 题目来源：[40. 组合总和 II](https://leetcode.cn/problems/combination-sum-ii)。

该题目与『组合总和』的区别是 **集合中的元素可能重复**，但要求 **最后的结果不能包含重复的组合**，该题目在解答时只需要在回溯的时候对对组合进行去重即可，去重的方法为：

~~~java
if (i > start && candidates[i] == candidates[i - 1]) {continue;}
~~~

#### [复原 IP 地址](https://leetcode-cn.com/problems/restore-ip-addresses)

##### 问题分析

1. **递归树**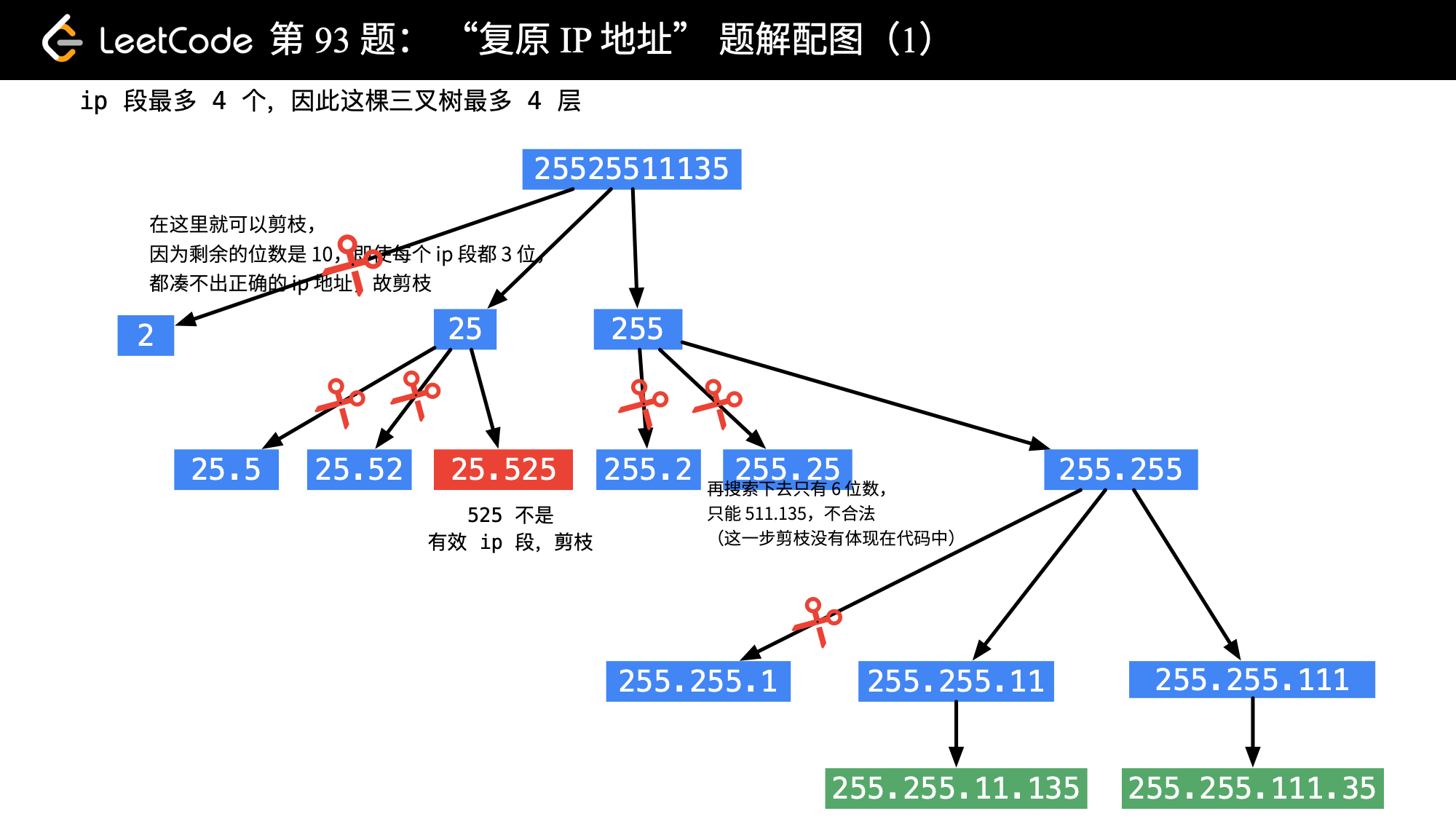：![「力扣」第 93 题：复原 IP 地址-1.png](https://notebook.ricear.com/media/202111/2021-11-09_2146160.4472708671924466.png)

1. 观察上图可知，**选择列表里的数**，**都是选择路径后面的数**，比如[255.255.11]这条路径，他后面的选择列表只有1、3、5，[255.255.111]这条路径，他后面的选择列表只有3、5，那么这个时候，**需要使用一个参数 `start`**，**来标识当前的选择列表的起始位置**。
   2. 同时，由于**整个ip字符串只能切分4段**（**有段数限制**），因此，还**需要一个参数 `split`**，**来标识当前字符串切分的次数**。
   3. 最终函数签名如下：

```java
      /**
       * 回溯算法求解复原 IP 地址问题
       * @param s 字符串
       * @param split 字符串切分次数
       * @param track 路径
       * @param start 每一次切分的起始位置
       */
      public void backtrack(String s, int split, LinkedList<String> track, int start)
      ```
2. **找结束条件**：

1. 如果**当前切分的起始位置等于字符串的长度**，就应该**直接返回**，而且如果**当前字符串切分次数刚好 4 次**，则**将路径按照 `.`进行拼接后**，**添加到结果列表中**：

```java
      int len = s.length();
      if (start == len) {
          if (split == 4) {
              res.add(String.join(".", track));
          }
          return;
      }
      ```
   2. 如果**剩下的字符串不够了或者超过剩余切分次数所需要字符串的最大限制**，则**直接返回**：

```java
      int left = len - start;
      if (left < (4 - split) || left > 3 * (4 - split)) {return;}
      ```
3. **找选择列表**：

```java
   for (int i = 0; i < 3; i++)
   ```
4. **判断是否需要剪枝**：

1. 如果在**从选择列表中选择元素时超过字符串长度**，则**直接返回**：

```java
      if (start + i >= len) {return;}
      ```
5. **做出选择**：

1. **将切分的节点添加到路径中**，并且**将切分的次数加1**，然后**从下一个字符开始截切分**：

```java
      track.add(ipSegment + "");
      backtrack(s, split + 1, track, start + i + 1);
      ```
6. **撤销选择**：

```java
   track.removeLast();
   ```

##### 参考代码

```java
//  最后结果
List<String> res = new ArrayList<>();

/**
 * 93. 复原 IP 地址
 * @param s 字符串
 * @return  所有可能从 s 获得的 有效 IP 地址
 */
public List<String> restoreIpAddresses(String s) {
    //  开始进行回溯
    LinkedList<String> track = new LinkedList<>();
    //  字符串切分次数
    int split = 0;
    //  每一次切分的起始位置
    int start = 0;
    backtrack(s, split, track, start);
    return res;
}

/**
 * 回溯算法求解复原 IP 地址问题
 * @param s 字符串
 * @param split 字符串切分次数
 * @param track 路径
 * @param start 每一次切分的起始位置
 */
public void backtrack(String s, int split, LinkedList<String> track, int start) {
    /**
     * 判断结束条件:
     *  1. 如果当前切分的起始位置等于字符串的长度，就应该直接返回，而且如果当前字符串切分次数刚好 4 次，则将路径按照 . 进行拼接后，添加到结果列表中
     *  2. 如果剩下的字符串不够了或者超过剩余切分次数所需要字符串的最大限制，则直接返回
     */
    int len = s.length();
    if (start == len) {
        if (split == 4) {
            res.add(String.join(".", track));
        }
        return;
    }

int left = len - start;
    if (left < (4 - split) || left > 3 * (4 - split)) {return;}

for (int i = 0; i < 3; i++) {
        //  如果超过字符串长度，则直接返回
        if (start + i >= len) {return;}

int ipSegment = judgeIfIpSegment(s, start, start + i);
        if (ipSegment != -1) {
            //  做选择：将节点添加到路径中
            track.add(ipSegment + "");
            backtrack(s, split + 1, track, start + i + 1);
            //  撤销选择：将节点从路径中移除
            track.removeLast();
        }
    }
}

/**
 * 判断截取的 ip 段是否符合要求
 * @param s 字符串
 * @param left  ip 段截取的起始位置
 * @param right ip 段截取的结束位置
 * @return  截取的 ip 段是否符合要求，如果符合，则返回截取的 ip 段，否则返回 -1
 */
public int judgeIfIpSegment(String s, int left, int right) {
    int len = right - left + 1;
    //  大于 1 位的时候，不能以 0 开头
    if (len > 1 && s.charAt(left) == '0') {return -1;}

//  转成 int 类型，并判断是否大于 255
    int res = 0;
    for (int i = left; i <= right; i++) {
        res = res * 10 + s.charAt(i) - '0';
    }
    if (res > 255) {return -1;}

return res;
}
```

### 全排列

#### 全排列

>题目来源：[46. 全排列](https://leetcode.cn/problems/permutations)。

##### 问题分析

1. **递归树**（最下面的叶子节点，红色框中的就是要求的结果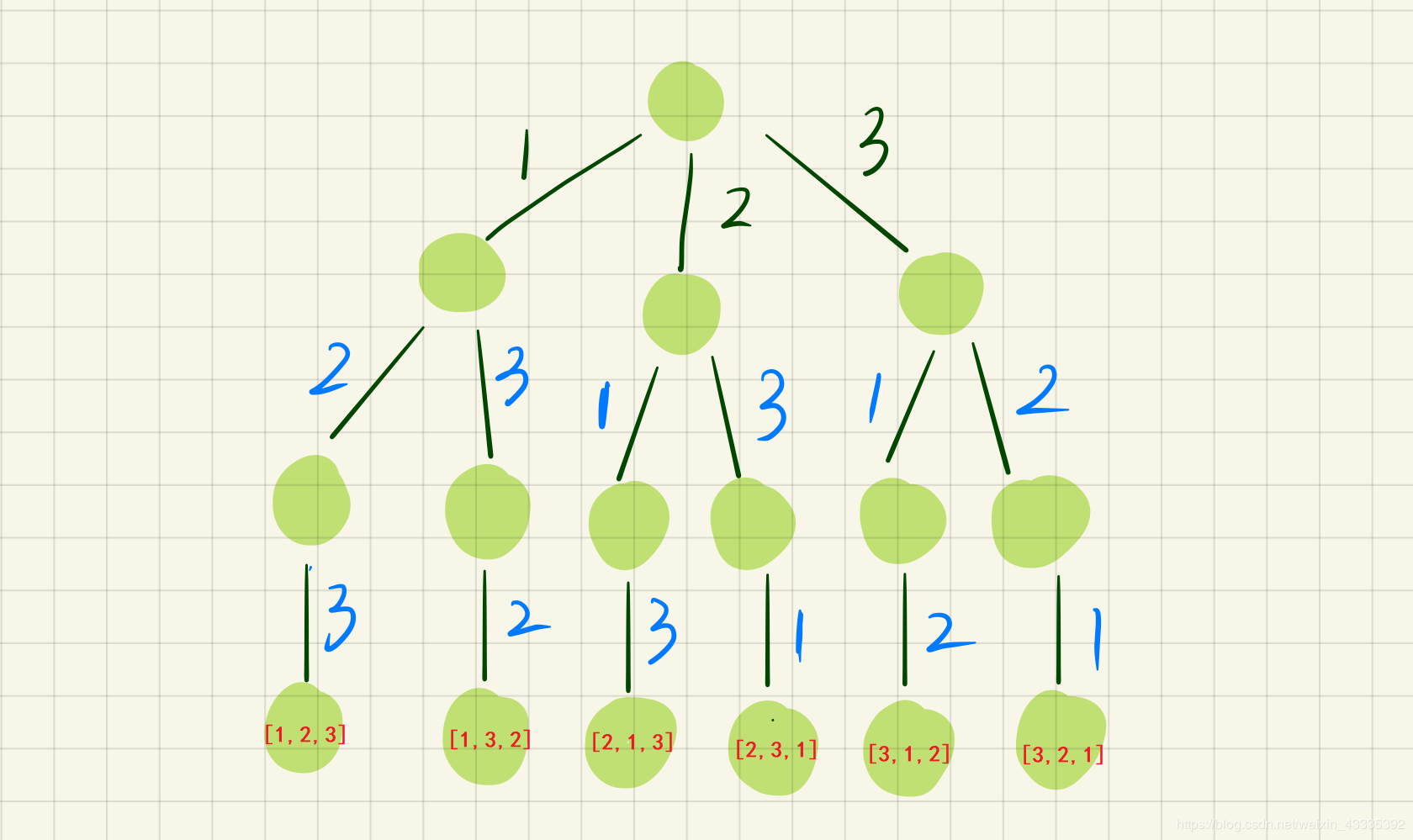）：![在这里插入图片描述](https://notebook.ricear.com/media/202108/2021-08-22_1951100.19782743043057216.png)

1. 绘制递归树的过程中，**如果我们选择了某个数**，**那么他的下一层的选择列表就是除去这个数以外的其他数**，比如，第一次选择了 2，那么他的下一层的选择列表只有 1 和 3；如果选择了 3，那么他的下一层的选择列表只有 1 和 2，那么这个时候就要**引入一个 `used` 数组来记录使用过的数字**，算法签名如下：

```java
      public void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used)
      ```
2. **找结束条件**：

```java
   if (nums.length == track.size()) {
       res.add(new LinkedList<>(track));
       return;
   }
   ```
3. **找准选择列表**：

```java
   for (int i = 0; i < nums.length; i++)
   ```
4. **判断是否需要剪枝**：

1. 如果当前节点已经使用过，则直接遍历下一个节点：

```java
      if (used[i]) {
          continue;
      }
      ```
5. **做出选择**：

```java
   track.add(nums[i]);
   used[i] = true;
   backtrack(nums, track, used);
   ```
6. **撤销选择**：

```java
   track.removeLast();
   used[i] = false;
   ```

##### 参考代码

```java
//  最后结果
List<List<Integer>> res = new LinkedList<>();

/**
 * 回溯算法解决全排列问题
 *  @param nums 数组
 * @param track 路径
 * @param used  是否使用过标识
 */
public void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
    if (nums.length == track.size()) {
        res.add(new LinkedList<>(track));
        return;
    }

for (int i = 0; i < nums.length; i++) {
        /**
         * 剪枝：
         *  1. 如果使用过，则遍历下一个节点
         */
        if (used[i]) {
            continue;
        }
        track.add(nums[i]);
        used[i] = true;
        backtrack(nums, track, used);
        track.removeLast();
        used[i] = false;
    }
}

/**
 * 46. 全排列
 *
 * @param nums 数组
 * @return 数组元素的全排列
 */
public List<List<Integer>> permute(int[] nums) {
    //  记录【路径】
    LinkedList<Integer> track = new LinkedList<>();
    boolean[] used = new boolean[nums.length];
    backtrack(nums, track, used);
    return res;
}
```

#### 全排列 II

> 题目来源：[47. 全排列 II](https://leetcode.cn/problems/permutations-ii)。

##### 问题分析

1. **递归树**：![在这里插入图片描述](https://notebook.ricear.com/media/202108/2021-08-22_2010350.651348149784578.png)
   1. 可以看到，有两组是重复的，这是因为在**选了第二个 2 后**，**又选了第一个 2**，从而**导致最右边整条分支都是重复的**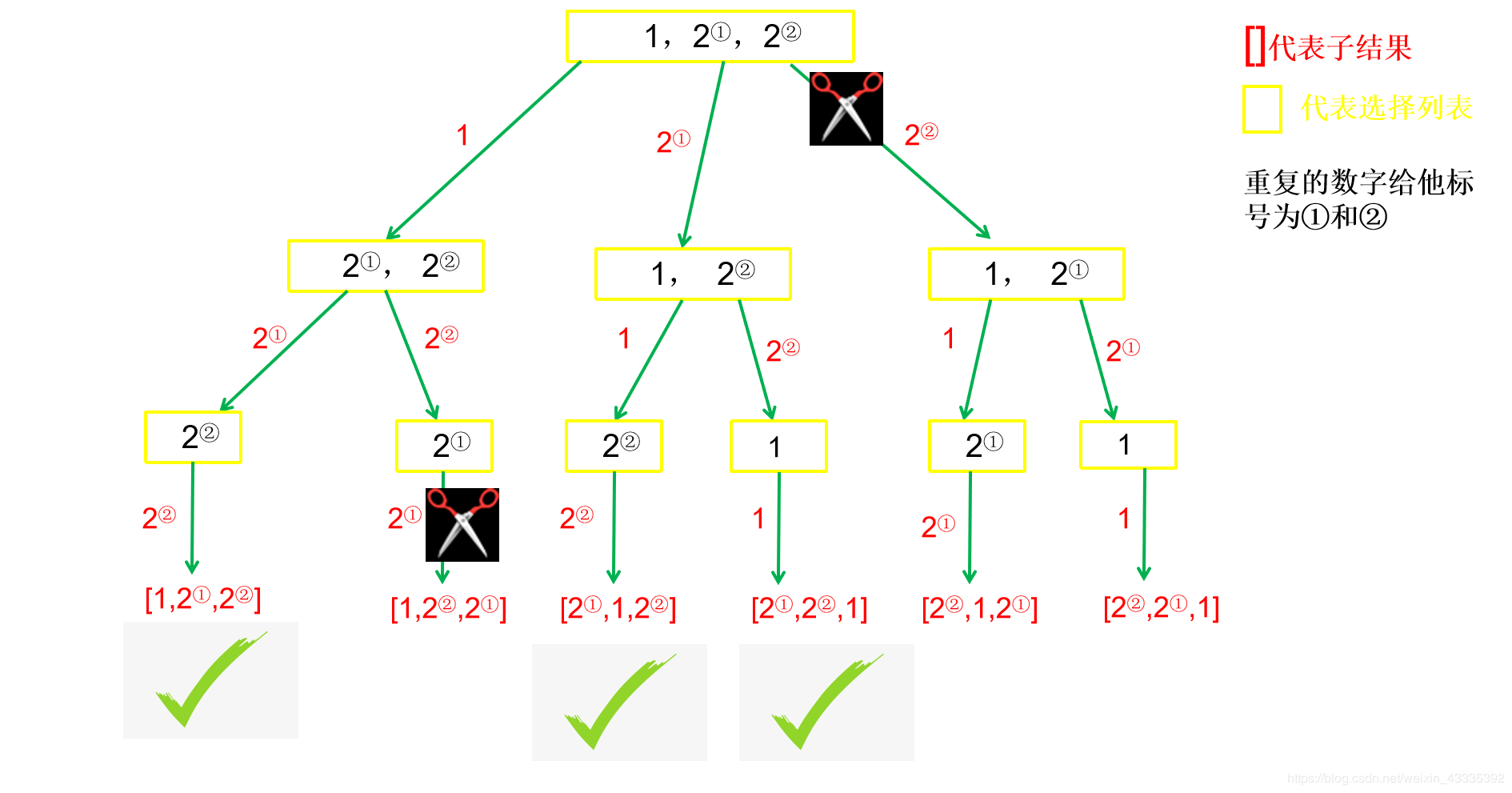：![在这里插入图片描述](https://notebook.ricear.com/media/202108/2021-08-22_2013540.367251238752221.png)
   2. 找结束条件和选择列表和前面差不多，这里不再赘述。
2. **判断是否需要剪枝**：
   1. 有了前面[子集、组合](#2-1-子集-组合)问题的判重经验，同样首先**要对题目中给出的 $nums$ 数组排序**，**让重复的元素并列排在一起**，在 `if(i > start && nums[i]==nums[i-1])` 基础上修改为 `if(i > 0 && nums[i]==nums[i-1] && !used[i-1])`，语义为**当 $i$ 可以选第一个元素之后的元素时**，**判断当前元素是否和上一个元素相同**，**如果相同**，**再判断上一个元素是否能用**，**如果上一个元素不能用**，那么**该分支一定是重复的**，**应该剪去**：

```java
      if (i > 0 && nums[i] == nums[i - 1] && used[i - 1]) {
      		continue;
      }
      ```
   2. 做出选择和撤销选择和上面类似，这里不再赘述。

##### 参考代码

```java
//  最终结果
List<List<Integer>> res = new ArrayList<>();

/**
 * 47. 全排列 II
 *
 * @param nums 数组
 * @return 所有不重复的全排列
 */
public List<List<Integer>> permuteUnique(int[] nums) {
    LinkedList<Integer> track = new LinkedList<>();
    boolean[] used = new boolean[nums.length];
    //  因为数组中有重复元素，而这些重复元素可能并不在一起（回溯算法中时通过数组中前后元素是否一致来判断子集是否重复的），从而可能导致后面结果出现重复的子集，因此需要先对子集进行排序，使得重复的元素都在一起
    Arrays.sort(nums);
    backtrack(nums, track, used);
    return res;
}

/**
 * 回溯法解决全排列问题
 *
 * @param nums  数组
 * @param track 路径
 * @param used  是否使用过标识
 */
public void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
    if (track.size() == nums.length) {
        List<Integer> list = new LinkedList<>(track);
        res.add(list);
        return;
    }

for (int i = 0; i < nums.length; i++) {
        /**
         * 剪枝：
         *  1. 如果使用过，则遍历下一个节点
         *  2. 如果当前节点和上一个节点的值相等，且上一个节点已经使用过，则当前排列全排列一定为重复的全排列，直接遍历下一个节点
         */
        if (used[i]) {
            continue;
        }
        if (i > 0 && nums[i] == nums[i - 1] && used[i - 1]) {
            continue;
        }
        track.add(nums[i]);
        used[i] = true;
        backtrack(nums, track, used);
        used[i] = false;
        track.removeLast();
    }
}
```

##### 扩展题目

###### 字符串的排列

> 题目来源：[剑指 Offer 38. 字符串的排列](https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof)。

1. 这个题目和[全排列 II](#2-2-2-全排列-II)类似，需要注意的是**字符串转数组**和**List 转数组**的问题：
   1. **字符串转数组**：

```java
      char[] arr = s.toCharArray();
      ```
   2. **List 转数组**：

```java
      List<String> res = new ArrayList<>();
      res.toArray(new String[res.size()]);
      ```
2. 参考代码：
   ```java
   //  最后结果
   List<String> res = new ArrayList<>();
   
   /**
    * 剑指 Offer 38. 字符串的排列
    *
    * @param s 字符串
    * @return 字符串中字符的所有排列
    */
   public String[] permutation(String s) {
       StringBuffer buffer = new StringBuffer();
       boolean[] used = new boolean[s.length()];
       //  因为数组中有重复元素，而这些重复元素可能并不在一起（回溯算法中时通过数组中前后元素是否一致来判断子集是否重复的），从而可能导致后面结果出现重复的子集，因此需要先对子集进行排序，使得重复的元素都在一起
       char[] arr = s.toCharArray();
       Arrays.sort(arr);
       backtrack(arr, buffer, used);
       return res.toArray(new String[res.size()]);
   }
   
   /**
    * 回溯法解决字符串的排列问题
    *
    * @param arr    数组
    * @param buffer 路径
    * @param used   是否使用过标识
    */
   public void backtrack(char[] arr, StringBuffer buffer, boolean[] used) {
       if (buffer.length() == arr.length) {
           res.add(buffer.toString());
           return;
       }
   
       for (int i = 0; i < arr.length; i++) {
           /**
            * 剪枝：
            *  1. 如果使用过，则遍历下一个节点
            *  2. 如果当前节点和上一个节点的值相等，且上一个节点已经使用过，则当前排列全排列一定为重复的全排列，直接遍历下一个节点
            */
           if (used[i]) {
               continue;
           }
           if (i > 0 && arr[i] == arr[i - 1] && used[i - 1]) {
               continue;
           }
           buffer.append(arr[i]);
           used[i] = true;
           backtrack(arr, buffer, used);
           used[i] = false;
           buffer.deleteCharAt(buffer.length() - 1);
       }
   }
   ```

## 参考文献

1. [回溯算法解题套路框架](https://labuladong.gitbook.io/algo/mu-lu-ye-3/mu-lu-ye/hui-su-suan-fa-xiang-jie-xiu-ding-ban)。
2. [C++ 总结了回溯问题类型 带你搞懂回溯算法(大量例题)](https://leetcode-cn.com/problems/subsets/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-gao-)。
3. [ 回溯算法（画图分析剪枝条件）](https://leetcode-cn.com/problems/restore-ip-addresses/solution/hui-su-suan-fa-hua-tu-fen-xi-jian-zhi-tiao-jian-by)。