🧮 Algorithm Notebook
1、算法准备
1.1 牛客网编程OJ的典型输入输出
2、算法框架
2.1 动态规划
2.1.1 斐波那契数列
2.1.2 背包问题
2.1.3 贪心算法
2.1.4 序列和数组类问题
2.1.5 编辑距离
2.1.6 高楼扔鸡蛋
2.1.7 股票问题系列通解
2.1.8 最长有效括号
2.1.9 剪绳子
2.1.10 正则表达式匹配
2.2 二分查找
2.2.1 二分查找框架
2.2.2 搜索旋转排序数组
2.3 链表
2.3.1 反转链表
2.3.2 相交链表
2.3.3 合并链表
2.3.4 链表中倒数第k个节点
2.3.5 复制带随机指针的链表
2.4 排序算法
2.4.1 常见排序算法
2.5 二叉树
2.5.1 二叉树遍历
2.5.2 岛屿问题
2.5.3 二叉树路径问题
2.5.4 构造二叉树
2.6 回溯算法
2.6.1 回溯算法解题框架
2.6.2 N皇后
2.7 数组
2.7.1 删除有序数组中的重复项
2.7.2 滑动窗口最大值
2.7.3 调整数组顺序使奇数位于偶数前面
2.7.4 螺旋矩阵
2.7.5 多数元素
2.7.6 最大数
2.7.7 和为s的两个数字
2.7.8 构建乘积数组
2.7.9 两数之和
2.8 字符串
2.8.1 最小覆盖子串
2.8.2 比较版本号
2.8.3 验证IP地址
2.8.4 基本计算器 II
2.8.5 字符串解码
2.8.6 移掉 K 位数字
2.8.7 无重复字符的最长子串
2.8.8 第一个只出现一次的字符
2.8.9 翻转字符串里的单词
2.8.10 字符串转换整数 (atoi)
2.8.11 字符串四则运算
2.9 栈
2.9.1 最小栈
2.9.2 弹出序列
2.10 数学
2.10.1 用 Rand7() 实现 Rand10()
2.10.2 只出现一次的数字
2.10.3 整数反转
2.10.4 求1+2+…+n
2.10.5 二进制中1的个数
2.10.6 幂运算
2.10.7 1~n 整数中 1 出现的次数
2.10.8 数字序列中某一位的数字
2.10.9 丑数
2.10.10 n个骰子的点数
2.10.11 圆圈中最后剩下的数字
2.10.12 不用加减乘除做加法
2.10.13 x 的平方根
2.11 设计
2.11.1 LRU 缓存机制
-
+
游客
注册
登录
序列和数组类问题
## 序列类问题 ### 最长递增子序列 > 题目来源:[300. 最长递增子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence)。 #### 题目 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 **示例 1:** ```txt 输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。 ``` **示例 2:** ```txt 输入:nums = [0,1,0,3,2,3] 输出:4 ``` **示例 3:** ```txt 输入:nums = [7,7,7,7,7,7,7] 输出:1 ``` **提示:** * 1 <= nums.length <= 2500 * -104 <= nums[i] <= 104 **进阶:** * 你可以设计时间复杂度为 O(n2) 的解决方案吗? * 你能将算法的时间复杂度降低到 O(n log(n)) 吗? #### 问题分析 **最长递增子序列**和一种叫做**Patience Game**的纸牌游戏有关,甚至有一种排序方法就叫做**Patience Sorting**(耐心排序)。该纸牌游戏的玩法如下: 1. 首先,给我们一副扑克牌,我们想遍历数组那样从左到右一张一张处理这些扑克牌,最终要把这些牌分成若干堆。  2. 处理这些扑克牌要遵循以下规则: 1. **只能把点数小的牌压到点数比他大的牌上。** 2. 如果当前牌**点数较大没有可以放置的堆**,则**新建一个堆**,把这张牌放进去。 3. 如果当前牌**有多个堆可供选择**,则选择**最左边的堆**放置(保证牌堆顶的牌有序)。 3. 比如说上述的扑克牌最终会被分成这样 5 堆(我们认为 $A$ 的值最大,而不是 1)。 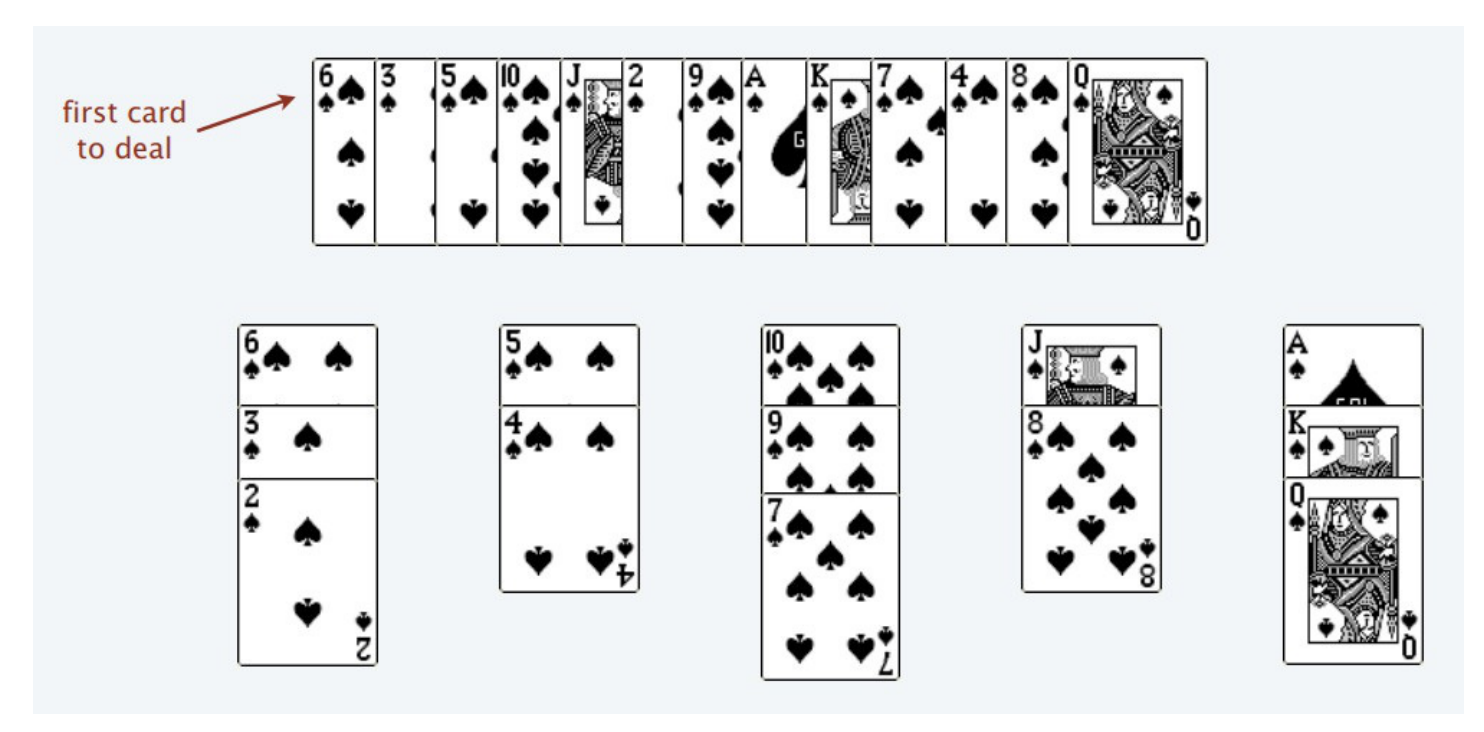 4. 按照上述规则执行,可以算出最长递增子序列,**牌的堆数就是最长递增子序列的长度**。 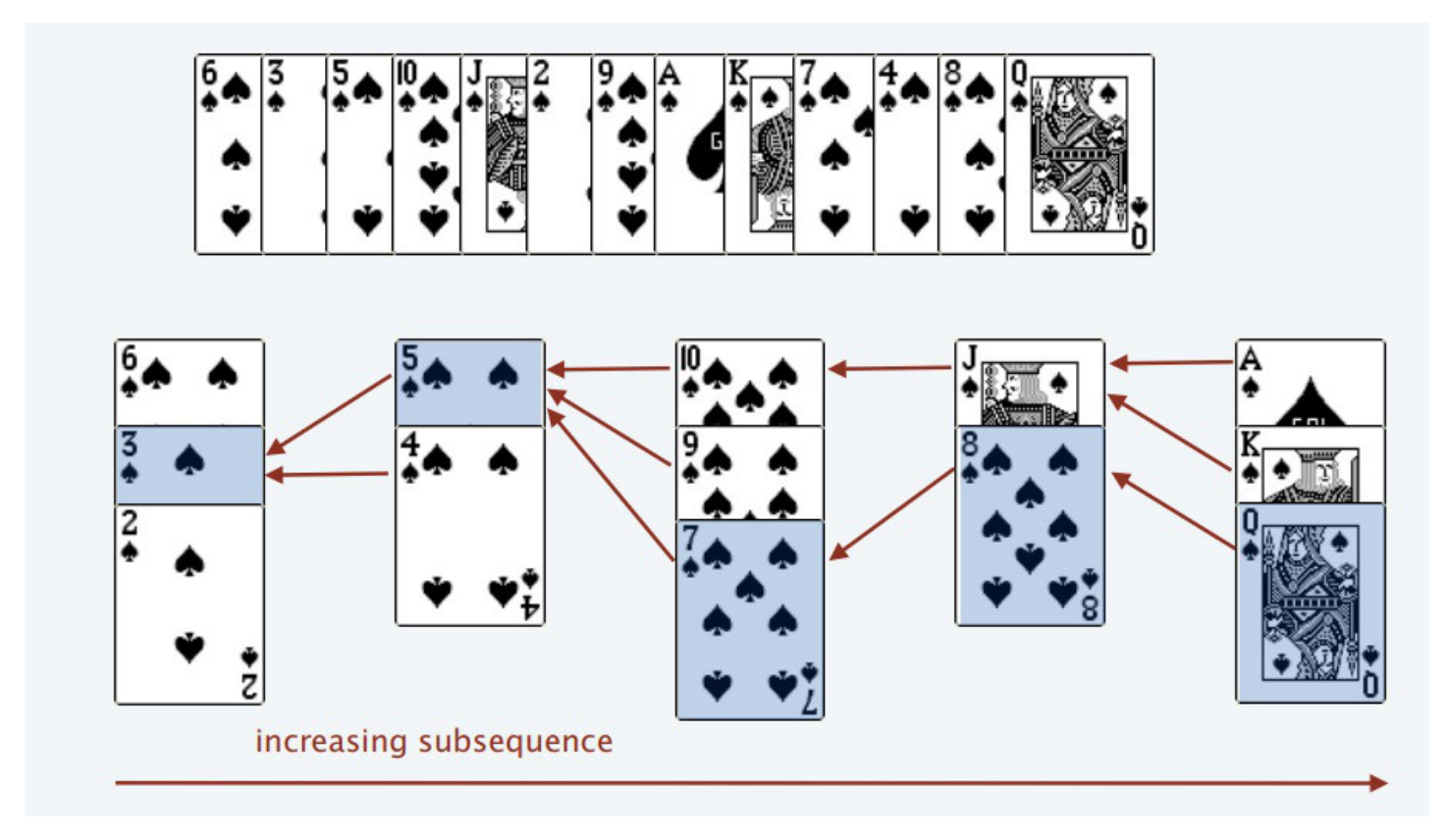 5. 我们只要把**处理扑克牌的过程**编程写出来即可。每次处理一张扑克牌不是要找到一个合适的牌堆顶来放吗,牌堆顶的牌不是有序吗,这就能用到[二分查找]()了:用**寻找左侧边界的二分查找法来搜索当前牌应放置的位置**。 #### 参考代码 ```java /** * 300. 最长递增子序列(版本 2:二分数组) * 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 * 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 * * @param nums 整数数组 * @return 最长严格递增子序列的长度 */ public int lengthOfLISV2(int[] nums) { // 牌堆顶部的牌 int[] top = new int[nums.length]; // 牌堆数 int piles = 0; // 遍历 nums,将牌进行分堆 for (int i = 0; i < nums.length; i++) { int poker = nums[i]; // 采用寻找左侧边界的二分查找法,寻找牌应放置的堆的位置 int left = 0, right = piles - 1; while (left <= right) { int mid = left + (right - left) / 2; if (top[mid] > poker) { right = mid - 1; } else if (top[mid] < poker) { left = mid + 1; } else if (top[mid] == poker) { right = mid - 1; } } // 没找到放牌的位置,则新建一堆 if (left >= piles) {piles++;}; // 将牌放到该堆的位置 top[left] = poker; } // 牌堆数即为最长递增子序列的长度,将其直接返回即可 return piles; } ``` #### 扩展题目 ##### 输出字典序最小的最长子序列 > 题目来源:[NC91 最长上升子序列(三)](https://www.nowcoder.com/practice/9cf027bf54714ad889d4f30ff0ae5481)。 ###### 问题解析 1. 解答此题时可以采用 [二分查找](https://notebook.ricear.com/project-21/doc-759) 的方法来进行求解。 2. 假设 $d[i]$ 表示 **长度为 $i$ 的最长上升子序列的末尾数字的最小值**,$p[i]$ 表示 **以 $arr[i]$ 为结尾的最长上升子序列的长度**: 1. 初始时最长上升子序列的长度 $len$ 为 1,$d[1] = arr[0]$,$p[0] = 1$。 2. 然后对数组进行遍历: 1. 如果 $arr[i]$ 大于 $d[len]$,表明 $arr[i]$ 可以与前面的元素组成一个 **更长的上升子序列**,因此将 $len$ 加 1,然后将 $arr[i]$ 赋值给 $d[len]$。 2. 否则,表明 $arr[i]$ **不能** 与前面的元素组成一个更长的上升子序列,此时需要看一下当前遍历到的元素是否可以与前面的元素组成一个 **字典序更小** 的最长上升子序列,实质上就是在 $d$ 中找到一个比 $arr[i]$ 更小的值,然后使用 $arr[i]$ 来替换 $d$ 中对应的元素,为了减少遍历所用的时间,这里采用 **二分查找** 的方法,问题也就转化为了二分查找的 **左侧边界** 的问题: 1. 初始时 $left$ 为 1,$right$ 为 $len$。 2. 如果 $d[mid]$ 小于 $arr[i]$: 1. $pos = mid$。 2. $left = mid + 1$。 3. 否则: 1. $right = mid - 1$。 4. 最后,更新 $d$ 中的相应的元素为 $arr[i]$ ,同时记录以 $arr[i]$ 结尾的最长上升子序列的长度: 1. $d[pos + 1] = arr[i]$。 2. $p[i] = pos + 1$。 > 💁 上面的 $pos$ 用来保存 $arr[i]$ 放到 $d$ 中的位置,也表示以 $arr[i]$ 结尾的最长上升子序列的长度。 > <iframe src="https://www.youtube.com/embed/FqPpFscQyzU?list=PLHH5EZ_Bw-YGWD--DBu0-jqb2ptqG_Igg" width="100%" height="480" allow="autoplay" allowfullscreen="true"></iframe> > 动画链接:[NC91-最长递增子序列](https://drive.google.com/file/d/1K2UPL4_H42Wn13ciXZ4wAeJDY7bplaKm/view?usp=sharing)。 ###### 参考代码 ```java /** * NC91-最长递增子序列 * * @param arr 数组 */ public int[] LIS (int[] arr) { if (arr.length == 1) {return arr;} // 特殊情况,[2] int[] d = new int[arr.length]; // d[i] 表示长度为 i 的最长递增子序列的末尾数字的最小值 int[] p = new int[arr.length]; // p[i] 表示以 arr[i] 为结尾的最长上升子序列的长度 int len = 1; d[len] = arr[0]; p[0] = 1; for (int i = 1; i < arr.length; i++) { if (arr[i] > d[len]) { d[++len] = arr[i]; p[i] = len; } else { int left = 1, right = len, pos = 0; while (left <= right) { int mid = left + (right - left) / 2; if (d[mid] < arr[i]) { pos = mid; left = mid + 1; } else { right = mid - 1; } } d[pos + 1] = arr[i]; p[i] = pos + 1; } } int[] ans = new int[len]; for (int i = p.length - 1; i >= 0; i--) { if (p[i] == len) { ans[--len] = arr[i]; } } return ans; } ``` ### 最长回文子序列 > 题目来源:[516. 最长回文子序列](https://leetcode-cn.com/problems/longest-palindromic-subsequence)。 #### 题目 给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。 **示例 1:** 输入: ``` "bbbab" ``` 输出: ``` 4 ``` 一个可能的最长回文子序列为 "bbbb"。 **示例 2:** 输入: ``` "cbbd" ``` 输出: ``` 2 ``` 一个可能的最长回文子序列为 "bb"。 **提示:** * 1 <= s.length <= 1000 * s 只包含小写英文字母 #### 解题思路 ##### 子序列问题处理模板 对于这种子序列问题,我们一般需要使用**动态规划**的方法来解决: 1. **找状态关系(通过数学归纳获得)。** 2. **定义 dp 数组(根据状态转移方程获得)。** dp 数组的定义主要有两种方式,一种是定义一个**一维数组**,另一种是定义一个**二维数组**。 ###### 一维 dp 数组 例如,在[最长递增子序列](http://notebook.ricear.com/project-21/doc-266)中,我们就是定义了一个一维数组,其含义为:**在子数组 $array[0..i]$ 中,我们要求的子序列(最长递增子序列)的长度是 $dp[i]$。** ```java int n = array.length; int[] dp = new int[n]; for (int i = 1; i < n; i++) { for (int j = 0; j < i; j++) { dp[i] = 最值(dp[i], dp[j] + ...) } } ``` ###### 二维 dp 数组 这种思路运用相对多一些,尤其是涉及两个字符串/数组的子序列。本思路中 dp 数组含义又分为**只涉及一个字符串**和**涉及两个字符串**两种情况。 1. **只涉及一个字符串/数组时:** 在子数组 $array[i..j]$ 中,我们要求的子序列(最长回文子序列)的长度为 $dp[i][j]$。 2. **涉及两个字符串/数组:在子数组 $arr1[0..i]$ 和 $arr2[0..j]$ 中,我们要求的子序列(最长公共子序列)长度为 $dp[i][j]$。** ##### 问题分析 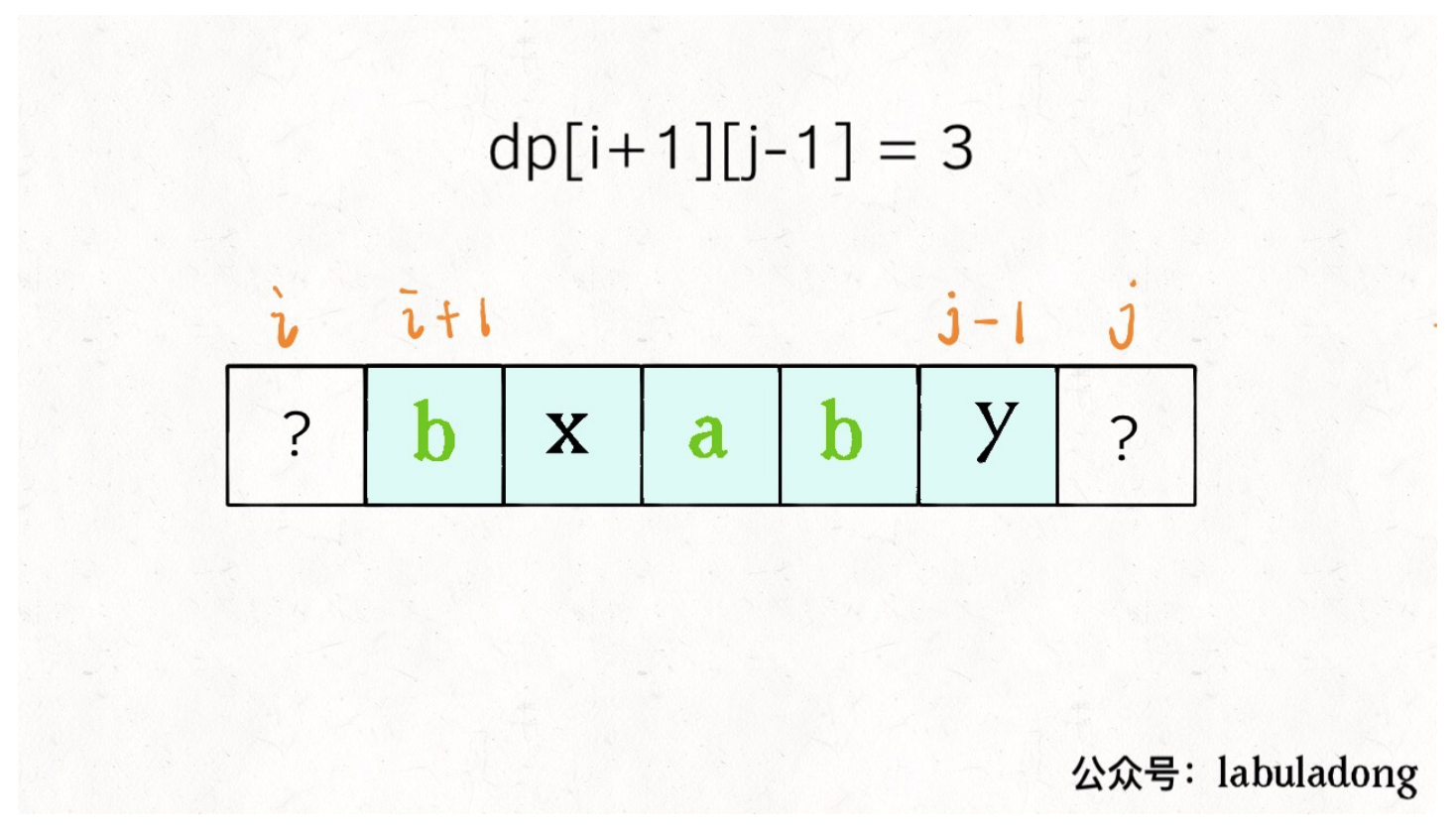 dp 函数的定义为:**在子串 $s[i..j]$ 中,最长回文子序列的长度为 $dp[i][j]$**。 如果我们想求 $dp[i][j]$,假设我们已经知道了子问题 $dp[i+1][j-1]$ 的结果,即 $s[i+1..j-1]$ 中最长回文子序列的长度,那么我们就可以想办法算出 $dp[i][j]$ 的值,即 $s[i..j]$ 中最长回文子序列的长度,这主要取决于 $s[i]$ 和 $s[j]$ 的字符。 1. **如果 $s[i]==s[j]$:** 则他俩加上 $s[i+1..j-1]$ 中的最长回文子序列就是 $s[i..j]$ 的最长回文子序列。  2. **如果 $s[i]!=s[j]$:** 说明他俩不可能同时出现在 $s[i..j]$ 的最长回文子序列中,那么把他俩分别加入 $s[i+1..j-1]$ 中,看看哪个子串产生的回文子序列更长即可。 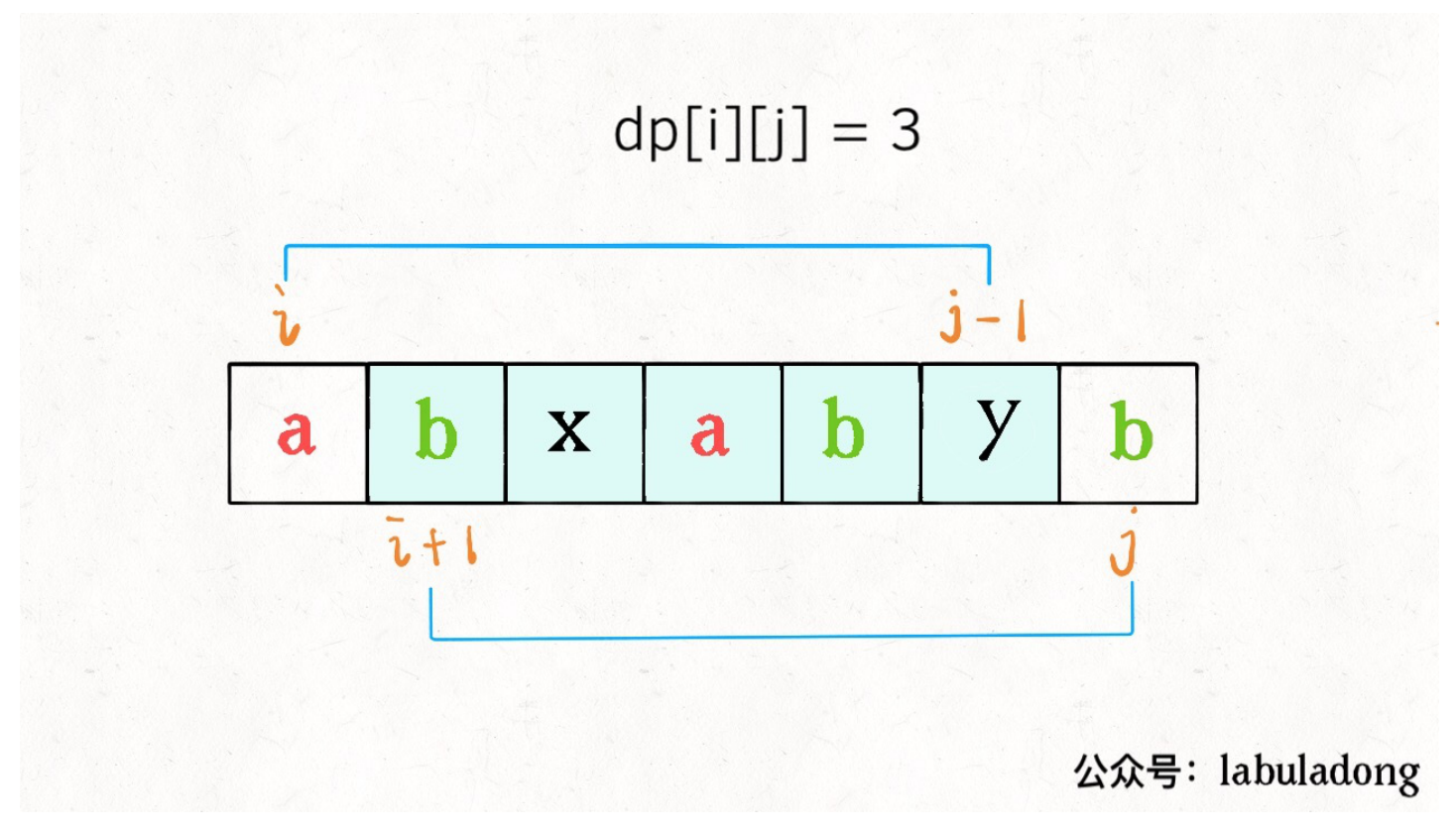 代码模板如下: ```c++ if (s[i] == s[j]) // 它俩⼀定在最⻓回⽂⼦序列中 dp[i][j] = dp[i + 1][j - 1] + 2; else // s[i+1..j] 和 s[i..j-1] 谁的回⽂⼦序列更⻓? dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); ``` 至此,状态转移方程就写出来了,根据**dp 数组**的定义,**我们要求的就是 $dp[0][n-1]$,也就是整个 s 的最长回文子序列的长度**。 ##### 参考代码 1. 首先明确一下 $base \space case$,如果只有一个字符,显然最长回文子序列的长度为 1,即 $dp[i][j]=1 \space (i==j)$。 2. 因为 $i$ 肯定小于 $j$,所以对于那些 $i>j$ 的位置,根本不存在什么子序列,应该初始化为 0。 3. 根据我们刚才的状态转移方程,想求 $dp[i][j]$ 需要知道 $dp[i+1][j-1]$,$dp[i+1][j]$,$dp[i][i-1]$ 这三个位置,将其填入 dp 数组后是这样: 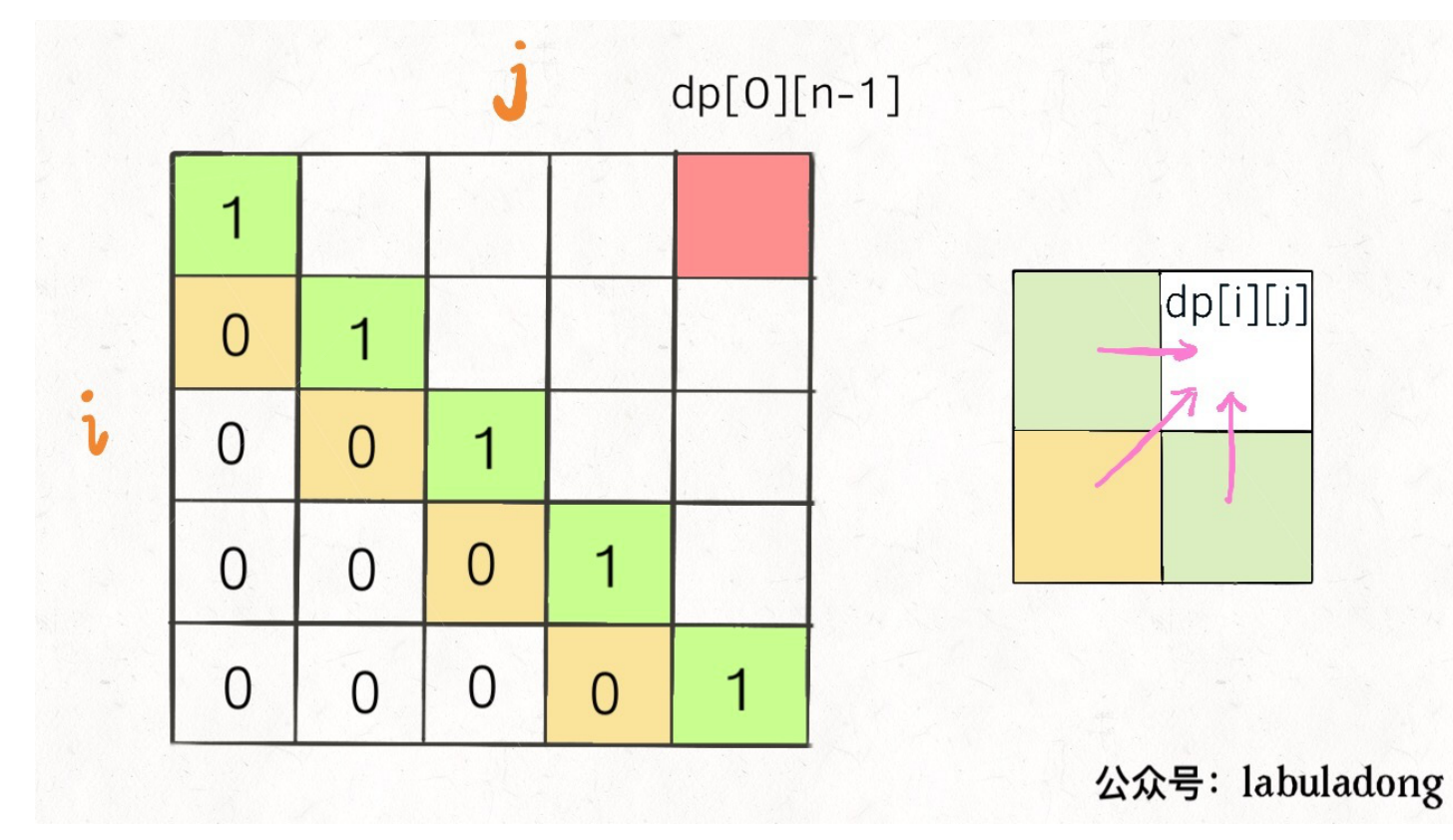 **为了保证每次计算 $dp[i][j]$,左、下、右方向的位置已经被计算出来了,只能斜着遍历或者反着遍历。** 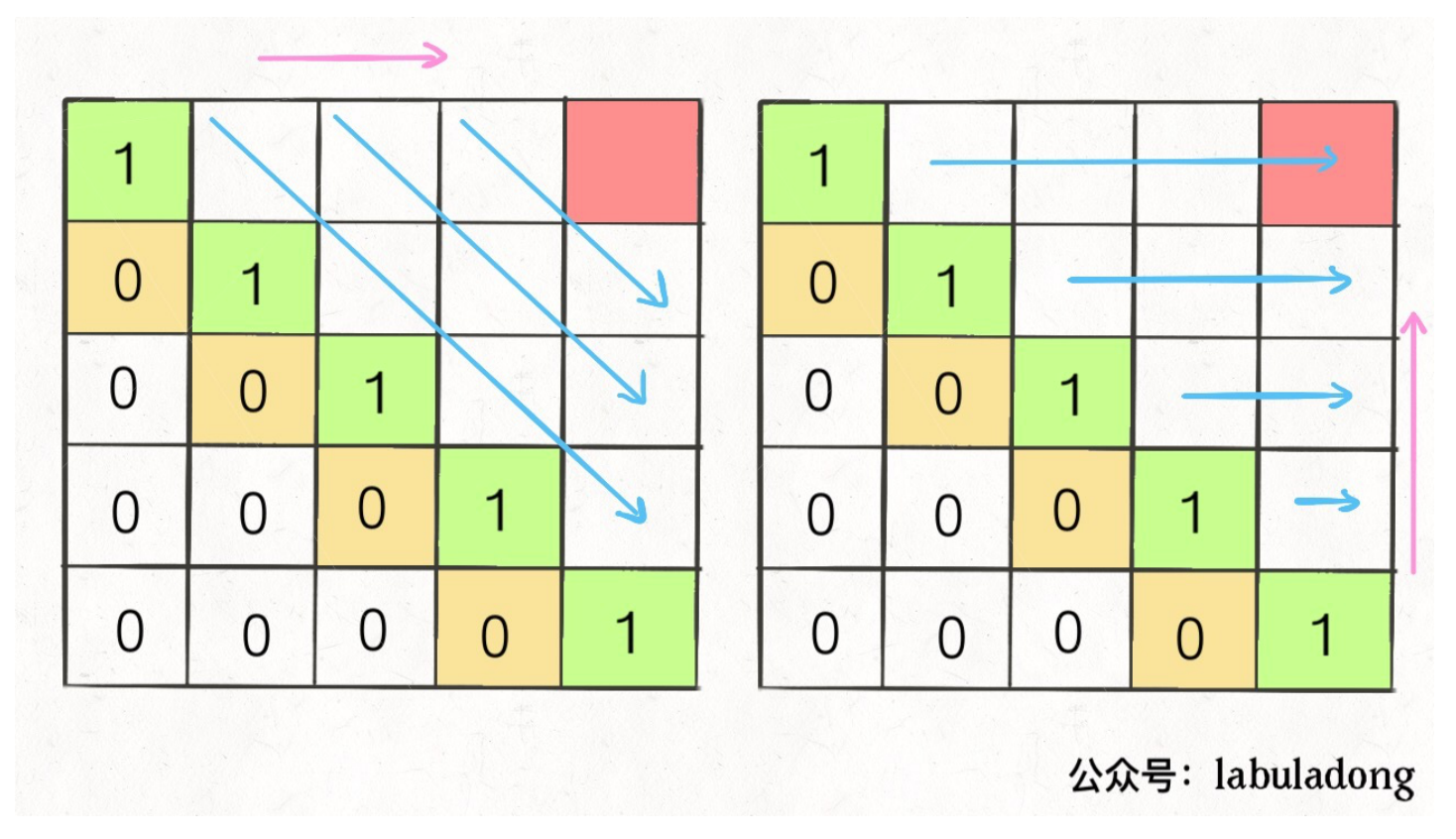 我选择**反着遍历**,参考代码如下: ```java package com.grayson.top; import java.util.Arrays; /** * @author peng.wei * @version 1.0 * @date 2021/4/8 14:50 * @Description 最长回文子序列 */ public class L516 { /** * 516. 最长回文子序列 * 给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。 * @param s 字符串 * @return 最长回文子序列的长度 */ public int longestPalindromeSubseq(String s) { int n = s.length(); // dp table: s[i...j] 子串的回文子序列的最大长度 // 最终的结果为 dp[0][n - 1] int[][] dp = new int[n][n]; // base case: 单个字符的回文子序列的最大长度为 1 for (int i = 0; i < n; i++) { dp[i][i] = 1; } for (int i = n - 1; i >= 0; i--) { for (int j = i + 1; j < n; j++) { if (s.charAt(i) == s.charAt(j)) { // 两个字符相等,将 dp[i + 1][j - 1] + 1 dp[i][j] = dp[i + 1][j - 1] + 2; } else { // 两个字符不相等,则 dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]) dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]); } } } // 返回最终的结果 dp[0][n - 1] return dp[0][n - 1]; } } ``` #### 扩展题目 ##### 最长回文子串 > 题目来源:[5. 最长回文子串](https://leetcode.cn/problems/longest-palindromic-substring)。 ###### 题目 给你一个字符串 s,找到 s 中最长的回文子串。 示例 1: ``` 输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。 ``` 示例 2: ``` 输入:s = "cbbd" 输出:"bb" ``` 示例 3: ``` 输入:s = "a" 输出:"a" ``` 示例 4: ``` 输入:s = "ac" 输出:"a" ``` ###### 问题分析 1. 可以通过对字符串进行遍历,然后在遍历的过程中 **以遍历到的字符为中心**,分 **奇数回文字符串** 和 **偶数回文字符串** 两种情况,采用 **双指针** 的方式来解决: 1. 假设当前遍历到的字符的下标为 $i$: 1. **奇数回文字符串**:第一个指针 $p$ 的起始位置为 $i - 1$,第二个指针 $q$ 的起始位置为 $i + 1$。 2. **偶数回文字符串**:第一个指针 $p$ 的起始位置为 $i - 1$,第二个指针 $q$ 的起始位置为 $i$。 2. 然后 $p$ 向 **左** 移动,$q$ 向 **右** 移动。 3. 结束循环的条件为(以下条件为 **或** 的关系): 1. $p$ **小于 0**。 2. $q$ **大于等于字符串的长度**。 3. $p$ 所在位置的字符和 $q$ 所在位置的 **字符不相等**。 2. 然后每次遍历更新最大的回文字符串为奇数回文字符串和偶数回文字符串中的最大值,当遍历结束后,返回最大的回文字符串即可。 ###### 参考代码 ```java /** * 寻找回文子串 * @param s 字符串 * @param start 起始字符的下标 * @param end 结束字符的下标 * @return 偶数回文子串的长度 */ public static String palindrome(String s, int start, int end) { int p = start, q = end; while (p >= 0 && q < s.length() && s.charAt(p) == s.charAt(q)) { p--; q++; } return s.substring(p + 1, q); } /** * 5.最长回文子串 * @param s 字符串 * @return 最长回文子串 */ public static String longestPalindrome(String s) { if (s.length() == 0) {return null;} else if (s.length() == 1) {return s;} String palindrome = ""; for (int i = 0; i < s.length(); i++) { String oddPalindrome = palindrome(s, i - 1, i + 1); String evenPalindrome = palindrome(s, i - 1, i); palindrome = oddPalindrome.length() > palindrome.length() ? oddPalindrome : palindrome; palindrome = evenPalindrome.length() > palindrome.length() ? evenPalindrome : palindrome; } return palindrome; } ``` ### 最长公共子序列 > 题目来源:[1143. 最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence)。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 类似的解法还可用于[1143. 最长公共子序列](https://leetcode-cn.com/problems/longest-common-subsequence/),不过这里和求最长重复子数组不同的一点是子序列中的元素不一定在原数组中连续,因此,在 $dp$ 数组的转换上稍微会有一定区别,具体如下: * **如果 $nums1[i] = nums2[j]$**,**则 $dp[i][j] = dp[i + 1][j + 1] + 1$**。 * **否则**,$dp[i][j] = max(dp[i + 1][j], dp[i][j + 1])$。 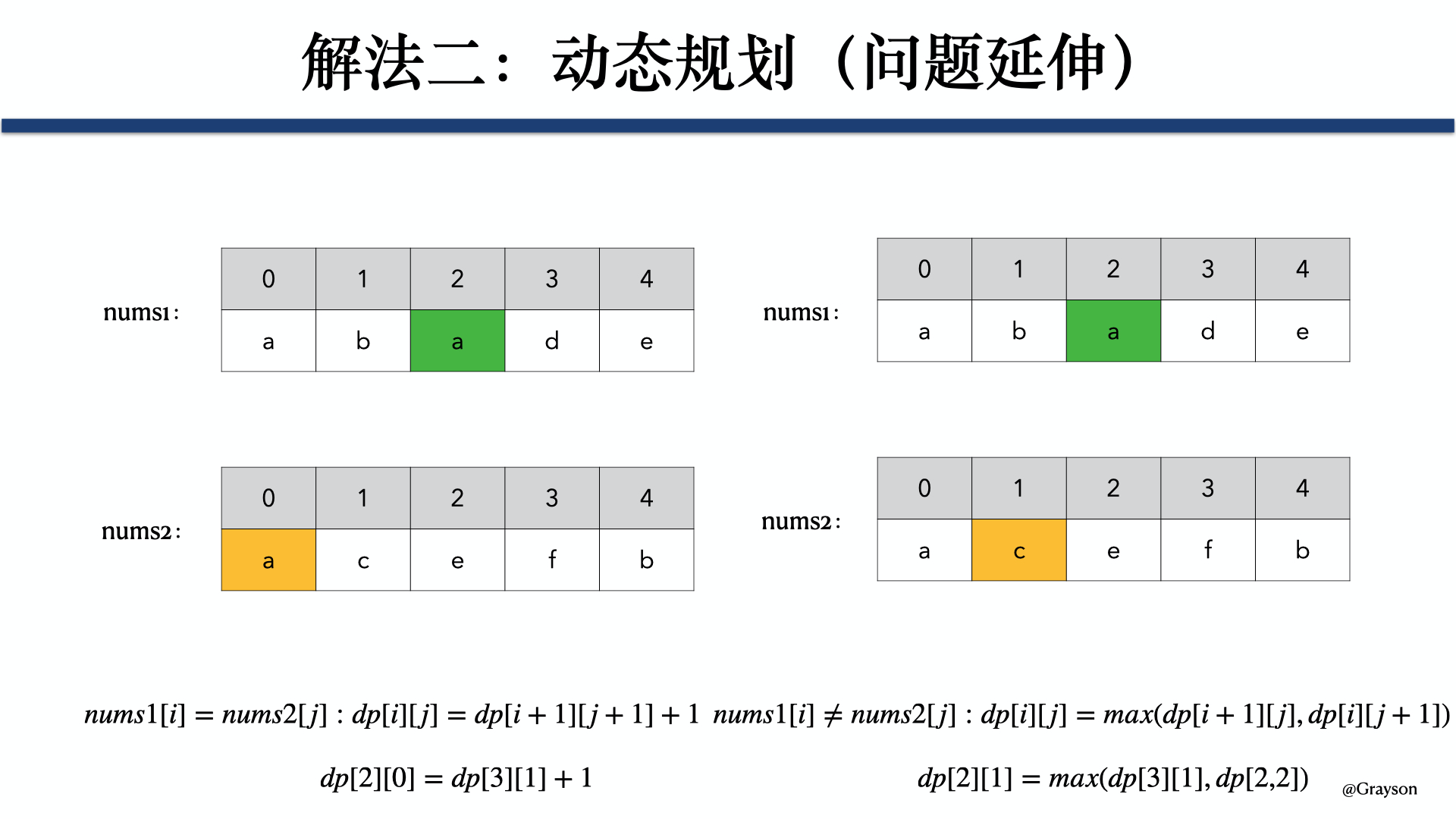 ###### 参考代码 ```java /** * 1143. 最长公共子序列 * @param text1 数组 1 * @param text2 数组 2 * @return 两个数组中公共的、长度最长的子数组的长度 */ public int longestCommonSubsequence(String text1, String text2) { int n1 = text1.length(); int n2 = text2.length(); int res = 0; // dp 数组,其中 dp[i][j] 表示 nums1[i:] 和 nums2[j:] 的最长公共子序列的长度,则 dp 数组中最大的元素即为 nums1 和 nums2 的最长公共子序列的长度 int[][] dp = new int[n1 + 1][n2 + 1]; // 分别遍历 nums1 和 nums2,计算最长公共子序列的长度 for (int i = n1 - 1; i >= 0; i--) { for (int j = n2 - 1; j >=0; j--) { // 如果 nums1[i] = nums2[j],则 dp[i][j] = dp[i + 1][j + 1],否则,dp[i][j] = max(dp[i + 1][j], dp[i][j + 1]) if (text1.charAt(i) == text2.charAt(j)) { dp[i][j] = dp[i + 1][j + 1] + 1; } else { dp[i][j] = Math.max(dp[i + 1][j], dp[i][j + 1]); } res = Math.max(res, dp[i][j]); } } // 返回结果 return res; } ``` ## 数组类问题 ### 最大子序和 > 题目来源:[53. 最大子序和](https://leetcode-cn.com/problems/maximum-subarray)。 #### 题目 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 **示例 1:** ```txt 输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。 ``` **示例 2:** ```txt 输入:nums = [1] 输出:1 ``` **示例 3:** ```txt 输入:nums = [0] 输出:0 ``` **示例 4:** ```txt 输入:nums = [-1] 输出:-1 ``` **示例 5:** ```txt 输入:nums = [-100000] 输出:-100000 ``` **提示:** * 1 <= nums.length <= 3 * 104 * -105 <= nums[i] <= 105 **进阶:** 如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 定义 $dp$ 数组: 1. $dp[i]$ 表示 $nums$ 中以 $nums[i]$ 结尾的最大子序和。 2. $dp[i]$ 中最大的元素即为 $nums$ 的最大子序和。 3. $dp[0] = nums[0]$。 2. 列出状态转移方程: $$ dp[i] = max(dp[i-1] + nums[i], nums[i]) $$  ###### 参考代码 ```java /** * 53. 最大子序和(版本 2:动态规划) * * @param nums 数组 * @return 最大子序和 */ public int maxSubArrayV2(int[] nums) { int len = nums.length, max; // dp 数组,其中 dp[i] 表示以 nums[i] 结尾的 nums[0...i] 序列中最大子序和 // 则最终 dp 数组中的最大值便是整个数组的最大子序和 int[] dp = new int[len]; dp[0] = nums[0]; max = dp[0]; for (int i = 1; i < len; i++) { dp[i] = Math.max(nums[i] + dp[i - 1], nums[i]); max = Math.max(max, dp[i]); } return max; } ``` ##### 贪心法 ###### 问题解析 1. 如果 sum 小于 0,说明他对于下一个 sum 起副作用,所以将 sum 重置为当前元素。 2. 否则的话,直接将当前元素累加到 sum 上。  ###### 参考代码 ```java /** * 53. 最大子序和(版本 3:贪心算法) * * @param nums 数组 * @return 最大子序和 */ public int maxSubArrayV3(int[] nums) { int sum = nums[0], max = nums[0]; int len = nums.length; for (int i = 1; i < len; i++) { if (sum < 0) { // 如果 sum 小于 0,说明他对于下一个 sum 起副作用,所以将 sum 重置为当前元素 sum = nums[i]; } else { // 否则的话,直接将当前元素累加到 sum 上 sum += nums[i]; } max = Math.max(max, sum); } return max; } ``` #### 扩展题目 ##### 返回最大和对应的子数组 ###### 问题分析 1. 可以**使用 $start$ 和 $end$ 来记录最大和对应的子数组区间**,**使用 $tmp\_start$ 和 $tmp\_end$ 作为从数组右侧往左侧遍历的过程中和递增的子数组区间**,然后**当更新 $res$ 值的时候用 $tmp\_start$ 和 $tmp\_end$ 来更新 $start$ 和**$end$。 ###### 参考代码 ```java /** * 53. 最大子序和(返回最大和对应的子数组) * * @param nums 数组 * @return 最大和对应的子数组 */ public int[] maxSubArray(int[] array) { int n = array.length, start = n - 1, end = n - 1, tmp_start = start, tmp_end = end; int[] dp = new int[n]; dp[n - 1] = array[n - 1]; int max = dp[n - 1]; /** * 获取最大和对应的子数组区间 */ for (int i = n - 2; i >= 0; i--) { if (array[i] > dp[i + 1] + array[i]) { // dp[i + 1] 为负数,说明 i 对应的元素为一个新的和递增的区间,因此需要更新 tmp_start 和 tmp_end tmp_start = i; tmp_end = i; dp[i] = array[i]; } else { // dp[i + 1] 为整数,说明 i 对应的元素和后面的元素依然是同一个和递增的区间,因此只需要更新 tmp_start 即可 tmp_start = i; dp[i] = dp[i + 1] + array[i]; } if (max <= dp[i]) { // 当前递增区间的和大于历史递增区间的和,因此需要用 tmp_start 和 tmp_end 来更新 start 和 end start = tmp_start; end = tmp_end; max = dp[i]; } } /** * 获取结果数组 */ int len = end - start + 1; int[] res = new int[len]; for (int i = 0; i < len; i++) { res[i] = array[start + i]; } return res; } ``` ### 打家劫舍 > 题目来源:[198. 打家劫舍](https://leetcode-cn.com/problems/house-robber)。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 该题目中 $dp$ 数组的含义为 $dp[i]$ 表示以从第 $i$ 家开始偷窃,在不触动警报装置的情况下,一夜之内能够偷窃得到的最高金额,且: $$ dp[i] = max(dp[i + 1], dp[i + 2] + nums[i]) $$ ###### 参考代码 ```java public int rob(int[] nums) { int m = nums.length; int[] dp = new int[m]; // base case if (m >= 1) {dp[m - 1] = nums[m - 1];} if (m >= 2) {dp[m - 2] = Math.max(nums[m - 1], nums[m - 2]);} for (int i = m - 3; i >= 0; i--) { dp[i] = Math.max(dp[i + 1], dp[i + 2] + nums[i]); } return dp[0]; } ``` ### 乘积最大子数组 > 题目来源:[152. 乘积最大子数组](https://leetcode-cn.com/problems/maximum-product-subarray)。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 对于这种**含有不定状态的最值问题**,一般可以通过**设置多个 $dp$ 数组来求解**,**分别用不同的 $dp$ 数组来表示不同的状态**。 2. 在本题中,假如我们直接**使用一个 $dp$ 数组**,其中 $dp[i]$**表示以第 $i$ 个元素结尾的最大连续子数组的乘积**,此时**当前位置的最优解未必是由前一个位置的最优解转移得到**。 3. 因此,我们可以**根据正负性进行讨论**: 1. 如果**当前位置是一个负数**的话,那么**我们希望以他前一个位置结尾的某个段的积也是个负数**,**这样就可以负负得正**,**并且我们希望这个积尽可能负得多**,即**尽可能小**。 2. 如果**当前位置是一个正数的话**,那么**我们希望以他前一个位置结尾的某个段的积也是个正数**,**并且我们希望这个积尽可能大**。 4. 因此我们需要**维护两个 $dp$ 数组**,**分别是 $dp_{max}$ 和**$dp_{min}$: 1. $dp_{max}$ 表示**以第 $i$ 个元素结尾的最大连续子数组的乘积**,且: $$ dp_{max} = max(dp_{max}[i - 1] \times nums[i], dp_{min}[i - 1] \times nums[i], nums[i]) $$ 2. $dp_{min}$ 表示**以第 $i$ 个元素结尾的最小连续子数组的乘积**,且: $$ dp_{min} = min(dp_{max}[i - 1] \times nums[i], dp_{min}[i - 1] \times nums[i], nums[i]) $$ ###### 参考代码 ```java /** * 152. 乘积最大子数组(版本 1:动态规划(优化前)) * * @param nums 数组 * @return 数组中乘积最大的连续子数组的乘积 */ public int maxProductV1(int[] nums) { int m = nums.length; // dp 数组,dpMax[i] 表示以第 i 个元素结尾的最大连续子数组的乘积 int[] dpMax = new int[m]; // dp 数组,dpMin[i] 表示以第 i 个元素结尾的最小连续子数组的乘积 int[] dpMin = new int[m]; int res; dpMax[0] = nums[0]; dpMin[0] = nums[0]; res = dpMax[0]; for (int i = 1; i < m; i++) { int item = nums[i]; // dpMax[i] = max(dpMax[i - 1] * nums[i], dpMin[i - 1] * nums[i], nums[i]) dpMax[i] = Math.max( dpMax[i - 1] * item, Math.max( dpMin[i - 1] * item, item ) ); // dpMin[i] = min(dpMax[i - 1] * nums[i], dpMin[i - 1] * nums[i], nums[i]) dpMin[i] = Math.min( dpMax[i - 1] * item, Math.min( dpMin[i - 1] * item, item ) ); // 去 dpMax 中的最大值 res = Math.max(res, dpMax[i]); } // 返回最后结果 return res; } ``` 由于**第 $i$ 个状态只和第 $i - 1$ 个状态相关**,根据**滚动数组**思想,我们可以**只用两个变量来维护 $i - 1$ 时刻的状态**,**一个维护 $dpMax$**,**一个维护 $dpMin$**。 ```java /** * 152. 乘积最大子数组(版本 2:动态规划(优化后)) * * @param nums 数组 * @return 数组中乘积最大的连续子数组的乘积 */ public int maxProductV2(int[] nums) { int m = nums.length; // dpMax 表示以第 i 个元素结尾的最大连续子数组的乘积 int dpMax = nums[0]; // dpMin 表示以第 i 个元素结尾的最小连续子数组的乘积 int dpMin = nums[0]; int res; res = dpMax; for (int i = 1; i < m; i++) { int item = nums[i]; int dpMaxTemp = dpMax, dpMinYemp = dpMin; // dpMax = max(dpMaxTemp * nums[i], dpMinYemp * nums[i], nums[i]) dpMax = Math.max( dpMaxTemp * item, Math.max( dpMinYemp * item, item ) ); // dpMin = min(dpMaxTemp * nums[i], dpMinYemp * nums[i], nums[i]) dpMin = Math.min( dpMaxTemp * item, Math.min( dpMinYemp * item, item ) ); // 去 dpMax 中的最大值 res = Math.max(res, dpMax); } // 返回最后结果 return res; } ``` ### 三角形最小路径和 > 题目来源:[120. 三角形最小路径和](https://leetcode-cn.com/problems/triangle)。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 该题目中 $dp$ 数组的含义为 $dp[i][j]$**表示从顶点到 $triangle.get(i).get(j)$ 的最小路径和**,且: $$ dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j - 1]) + triangle.get(i).get(j) $$ ###### 参考代码 ```java /** * 120. 三角形最小路径和 * * @param triangle 三角形顶点列表 * @return 三角形自顶向下的最小路径和 */ public int minimumTotal(List<List<Integer>> triangle) { int m = triangle.size(); int n = triangle.get(m - 1).size(); // dp 数组,其中 dp[i][j] 表示从顶点到 triangle.get(i).get(j) 的最小路径和 int[][] dp = new int[m][n]; int res = Integer.MAX_VALUE; for (int i = 0; i < m; i++) { for (int j = 0; j < triangle.get(i).size(); j++) { int item = triangle.get(i).get(j); // 转移关系为:dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j - 1]) + triangle.get(i).get(j) // 需要确保数组下标不要越界,即:i - 1 >= 0 && j - 1 >= 0 && j < triangle.get(i - 1).size() if (i - 1 >= 0) { if (j - 1 >= 0) { if (j < triangle.get(i - 1).size()) { dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j - 1]) + item; } else { dp[i][j] = dp[i - 1][j - 1] + item; } } else { dp[i][j] = dp[i - 1][j] + item; } } else { dp[i][j] = item; } } } // 三角形最后一行中的最小路径和即为整个三角形自顶向下的最小路径和 for (int i = 0; i < triangle.get(m - 1).size(); i++) { res = Math.min(res, dp[m - 1][i]); } return res; } ``` ### 解码方法 > 题目来源:[91. 解码方法](https://leetcode-cn.com/problems/decode-ways)。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 动态规划中: 1. 对于**一维 $dp$ 数组**一般**有两种思路**,**一种是以 $nums[i]$ 开头**,**另一种是以 $nums[i]$ 结尾**,我们在定义 $dp$ 数组时可以**从这两个方面去考虑**即可。 2. 对于**二维 $dp$ 数组**一般**可以从中间进行截取**,例如[1.1.7 最长回文子序列](https://notebook.ricear.com/project-21/doc-273)中 $dp$ 数组的定义为 $dp[i][j]$ 表示 $s[i...j]$ 中包含的最长回文子序列的长度。 2. 该题目中 $dp$ 数组的含义为 $dp[i]$ 表示以 $s.charAt(i)$ 开头的字符串的解码方法的总数,且: $$ dp[i] = dp[i + 1] + dp[i + 2] $$ ###### 参考代码 ```java /** * 91. 解码方法 * * @param s 消息字符串 * @return 消息字符串解码方法的总数 */ public int numDecodings(String s) { int m = s.length(); // dp 数组,其中 dp[i] 表示以 s.charAt(i) 开头的消息字符串解码方法的总数 int[] dp = new int[m]; for (int i = m - 1; i >= 0; i--) { // 如果当前字符为 0,那么以该字符开头的字符串的解码方法总数为 0 if (s.charAt(i) == '0') {dp[i] = 0;} // 如果当前字符不为 0,并且当前字符位于最后一个位置,那么以该字符开头的字符串的解码方法总数为 1 else if (i == m - 1) {dp[i] = 1;} // 当前字符不为 0,并且当前字符位于倒数第二个位置 else if (i == m - 2) { // 如果当前字符及其后两位所组成的数字大于 26,则当前字符及其后两位字符组成的字符串不能被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数 if (Integer.parseInt(s.substring(i, i + 2)) > 26) {dp[i] = dp[i + 1];} // 如果当前字符及其后两位所组成的数字不大于 26,则当前字符及其后两位字符组成的字符串可以被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数加 1 else {dp[i] = dp[i + 1] + 1;} } // 当前字符不为 0,并且当前字符不位于倒数第二个位置 // 如果当前字符及其后两位所组成的数字大于 26,则当前字符及其后两位字符组成的字符串不能被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数 else if (Integer.parseInt(s.substring(i, i + 2)) > 26) {dp[i] = dp[i + 1];} // 如果当前字符及其后两位所组成的数字不大于 26,则当前字符及其后两位字符组成的字符串可以被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数及以下面第二个字符开头的字符串的解码方法总数 else {dp[i] = dp[i + 1] + dp[i + 2];} } // 返回最后的结果 return dp[0]; } ``` #### 扩展题目 ##### 把数字翻译成字符串 > 题目来源:[剑指 Offer 46. 把数字翻译成字符串](https://leetcode.cn/problems/ba-shu-zi-fan-yi-cheng-zi-fu-chuan-lcof)。 ###### 问题分析 1. 参见[解码方法](#2-5-1-1-1-问题分析)。 ###### 参考代码 ```java /** * 剑指 Offer 46. 把数字翻译成字符串 * @param num 待翻译的数字 * @return 数字翻译后的字符串 */ public int translateNum(int num) { String s = String.valueOf(num); int m = s.length(); // dp 数组,其中 dp[i] 表示以 s.charAt(i) 开头的消息字符串解码方法的总数 int[] dp = new int[m]; for (int i = m - 1; i >= 0; i--) { // 如果当前字符位于最后一个位置,那么以该字符开头的字符串的解码方法总数为 1 if (i == m - 1) {dp[i] = 1;} // 当前字符位于倒数第二个位置 else if (i == m - 2) { // 如果当前字符及其后两位所组成的数字大于 25 或当前字符为 0,则当前字符及其后两位字符组成的字符串不能被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数 if (Integer.parseInt(s.substring(i, i + 2)) > 25 || s.charAt(i) == '0') {dp[i] = dp[i + 1];} // 如果当前字符及其后两位所组成的数字不大于 26,则当前字符及其后两位字符组成的字符串可以被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数加 1 else {dp[i] = dp[i + 1] + 1;} } // 当前字符不位于倒数第二个位置 // 如果当前字符及其后两位所组成的数字大于 25 或当前字符为 0,则当前字符及其后两位字符组成的字符串不能被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数 else if (Integer.parseInt(s.substring(i, i + 2)) > 25 || s.charAt(i) == '0') {dp[i] = dp[i + 1];} // 如果当前字符及其后两位所组成的数字不大于 25,则当前字符及其后两位字符组成的字符串可以被解码, // 以该字符开头的字符串的解码方法总数等于以下一个字符开头的字符串的解码方法总数及以下面第二个字符开头的字符串的解码方法总数 else {dp[i] = dp[i + 1] + dp[i + 2];} } // 返回最后的结果 return dp[0]; } ``` ### 打家劫舍 II > 题目来源:[213. 打家劫舍 II](https://leetcode-cn.com/problems/house-robber-ii)。 #### 解题思路 ##### 动态规划 ###### 问题分析 1. 对于这种**圆环型**的问题,我们可以**把他拆分成两部分**,并对其**分别去求结果**,然后再**将两部分的结果取最值**即可。 2. 该题目中 $dp$ 数组的含义为 $dp[i]$ 表示第 $i$ 户及之后所能偷到的最大金额,且: $$ dp[i] = max(dp[i + 1], dp[i + 2] + nums[i]); $$ ###### 参考代码 ```java /** * 213. 打家劫舍 II * @param nums 每个房屋存放金额的非负整数数组 * @return 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额 */ public int rob(int[] nums) { int m = nums.length; // 将整个数组拆分成两部分,分别为 nums[0, nums.length - 2] 和 nums[1, nums.length - 1],然后对这两部分分别求能够偷窃到的最大金额,并取二者的最大值即可 return m > 1 ? Math.max(subRob(nums, 0, m - 1), subRob(nums, 1, m)) : nums[0]; } /** * 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额 * @param nums 每个房屋存放金额的非负整数数组 * @param start 起始位置 * @param end 结束位置 * @return 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额 */ public int subRob(int[] nums, int start, int end) { int m = nums.length; // dp 数组,其中 dp[i] 表示从第 i 户及后面住户中所能偷窃到的最高金额 int[] dp = new int[m]; // base case if (end >= 1) { dp[end - 1] = nums[end - 1]; } if (end >= 2) { if (nums[end - 2] >= nums[end - 1]) { dp[end - 2] = nums[end - 2]; } else { dp[end - 2] = nums[end - 1]; } } for (int i = end - 3; i >= start; i--) { // 第 i 户及之后所能偷到的最大金额 等于 第 i 户及之后所能偷到的最大金额 与 第 i + 2 户所能偷到的最大金额和第 i 户金额之和 的最大值 dp[i] = Math.max(dp[i + 1], dp[i + 2] + nums[i]); } return dp[start]; } ``` ### 最长重复子数组 > 题目来源:[718. 最长重复子数组](https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray)。 > 类似的题目还有: > > 1. [NC127 最长公共子串](https://www.nowcoder.com/practice/f33f5adc55f444baa0e0ca87ad8a6aac)。 > 如果需要返回最长重复子数组的元素,则尽量采用 **滑动窗口** 的方法。 ##### 动态规划 ###### 问题分析 1. 对于求**最值**的题目,都可以思考一下看是否可以用**动态规划**来求解,而**动态规划的核心就是定义 $dp$ 数组**,**寻找状态转移方程**。 2. $dp$**数组的定义有一维和二维数组两种**,这个**需要根据具体的题目来具体分析**。 3. 本题中 $dp$ 数组可以定义为 $dp[i][j]$,**表示 $nums1[i]$ 和 $nums2[j]$ 的最长公共前缀的长度**,这样 $dp$**数组中最大的元素即为 $nums1$ 和 $nums2$ 的最长重复子数组的长度**。 4. 然后分别遍历 $nums1$ 和 $nums2$: 1. **如果 $nums1[i] = nums2[j]$**,**则 $dp[i][j] = dp[i + 1][j + 1] + 1$**。 2. **否则**,$dp[i][j] = 0$。 > 该题目类似于[最长公共子序列](#1-3-最长公共子序列),不同的是在最长公共子序列中当 $nums1[i] \ne nums2[j]$ 时,$dp[i][j] = max(dp[i + 1][j], dp[i][j + 1])$,而在最长重复子数组中当 $nums1[i] \ne nums2[j]$ 时,$dp[i][j] = 0$,这是因为**序列不要求连续**,而**数组要求连续**。 > 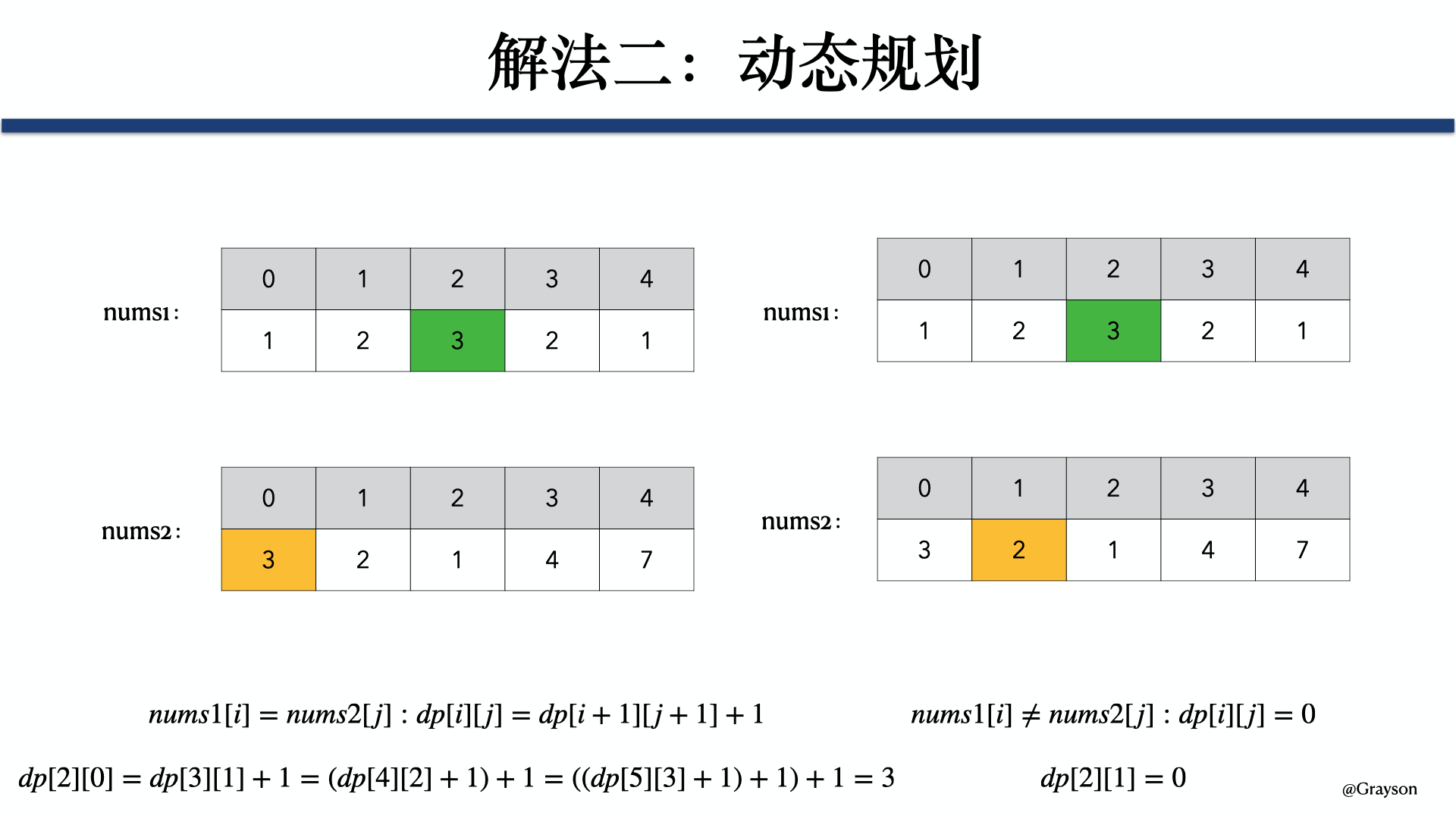 ###### 参考代码 ```java /** * 718. 最长重复子数组(版本 2:动态规划) * @param nums1 数组 1 * @param nums2 数组 2 * @return 两个数组中公共的、长度最长的子数组的长度 */ public int findLengthV2(int[] nums1, int[] nums2) { int n1 = nums1.length; int n2 = nums2.length; int res = 0; // dp 数组,其中 dp[i][j] 表示 nums1[i:] 和 nums2[j:] 的最长公共前缀的长度,则 dp 数组中最大的元素即为 nums1 和 nums2 的最长重复子数组的长度 int[][] dp = new int[n1 + 1][n2 + 1]; // 分别遍历 nums1 和 nums2,计算最长重复子数组的长度 for (int i = n1 - 1; i >= 0; i--) { for (int j = n2 - 1; j >=0; j--) { // 如果 nums1[i] = nums2[j],则 dp[i][j] = dp[i + 1][j + 1],否则,dp[i][j] = 0 dp[i][j] = (nums1[i] == nums2[j] ? dp[i + 1][j + 1] + 1 : 0); res = Math.max(res, dp[i][j]); } } // 返回结果 return res; } ``` ##### 滑动窗口 ###### 问题分析 1. 对于**两个数组的遍历**,可以**通过滑动窗口的方法来减少遍历的次数**,因为**每次比较的只是滑动窗口内部相同区域的元素**,**相比于暴力解法而言**,**可以显著减少遍历的次数**。 2. 本题目中可以先**把 $nums1$ 放在上面**,$nums2$**放在下边**,然后**将 $nums1$ 的第一个元素和 $nums2$ 的最后一个元素对齐**,然后**将 $nums2$ 从做往右滑动**,**直到 $nums1$ 的第一个元素和 $nums2$ 的第一个元素对齐**,且**每滑动一次**,**都对两个数组滑块内部相同区域的元素进行比较**。 3. 然后**把 $nums2$ 放在上面**,$nums1$**放在下面**,并且**把 $nums2$ 的第一个元素和 $nums1$ 的第一个元素对齐**,然后**把 $nums1$ 从右往左滑动**,**直到 $nums2$ 的第一个元素和 $nums1$ 的最后一个元素对齐**,且**每滑动一次**,**都对两个数组滑块内部相同区域的元素进行比较**。 4. 其实**第三步可以合到第二步里面**,即**在第二步中一直把 $nums2$ 滑动到第一个元素和 $nums1$ 的第一个元素对齐**,但这样**不太好实现**,因此**后面一步拆分成等价的第四步来实现**。 _1626441966.gif) ###### 参考代码 ```java /** * 718. 最长重复子数组(版本 3:滑动窗口) * @param nums1 数组 1 * @param nums2 数组 2 * @return 两个数组中公共的、长度最长的子数组的长度 */ public int findLengthV3(int[] nums1, int[] nums2) { int n1 = nums1.length; int n2 = nums2.length; int res = 0; // nums1 的第一个元素和 nums2 的最后一个元素对齐,然后将 num2 从左往右滑动,直到 nums2 的第一个元素和 nums1 的第一个元素对齐 for (int i = n2 - 1; i >= 0; i--) { int minLen = Math.min(n1, n2 - i); int tempRes = 0; // 遍历 nums1 和 nums2 交叉的部分,并计算这一部分的最长重复子数组的长度 for (int j = 0; j < minLen; j++) { if (tempRes != 0 && nums1[j] != nums2[i + j]) { res = Math.max(res, tempRes); tempRes = 0; } if (nums1[j] == nums2[i + j]) { tempRes++; } } res = Math.max(res, tempRes); } // nums2 的第一个元素和 nums1 的第一个元素对齐,然后将 num1 从右往左滑动,直到 nums2 的第一个元素和 nums1 的最后一个元素对齐 for (int i = 0; i < n1; i++) { int minLen = Math.min(n1 - i, n2); int tempRes = 0; // 遍历 nums1 和 nums2 交叉的部分,并计算这一部分的最长重复子数组的长度 for (int j = 0; j < minLen; j++) { if (tempRes != 0 && nums1[i + j] != nums2[j]) { res = Math.max(res, tempRes); tempRes = 0; } if (nums1[i + j] == nums2[j]) { tempRes++; } } res = Math.max(res, tempRes); } return res; } ``` ## 参考文献 1. [动态规划设计:最长递增子序列](https://labuladong.gitbook.io/algo/mu-lu-ye-2/mu-lu-ye-1/dong-tai-gui-hua-she-ji-zui-chang-di-zeng-zi-xu-lie)。 2. [动态规划之子序列问题解题模板](https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/zi-xu-lie-lei-xing-wen-ti/zi-xu-lie-wen-ti-mo-ban)。 3. [最大子序和 c++ 实现四种解法 暴力法、动态规划、贪心法和分治法 图示讲解](https://leetcode-cn.com/problems/maximum-subarray/solution/zui-da-zi-xu-he-cshi-xian-si-chong-jie-fa-bao-li-f)。 4. [乘积最大子数组](https://leetcode-cn.com/problems/maximum-product-subarray/solution/cheng-ji-zui-da-zi-shu-zu-by-leetcode-solution)。 5. [最长重复子数组](https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray/solution/zui-chang-zhong-fu-zi-shu-zu-by-leetcode-solution)。 6. [滑动窗口解法](https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray/solution/wu-li-jie-fa-by-stg-2)。 7. [题解 | #最长递增子序列#](https://www.nowcoder.com/practice/9cf027bf54714ad889d4f30ff0ae5481?tpId=117&tqId=37796&rp=1&ru=/exam/oj&qru=/exam/oj&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D117&difficulty=undefined&judgeStatus=undefined&tags=&title=)。
ricear
2022年7月22日 20:47
©
BY-NC-ND(4.0)
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
分享
链接
类型
密码
更新密码